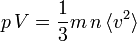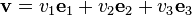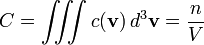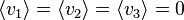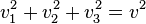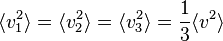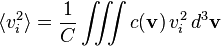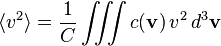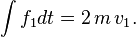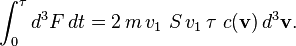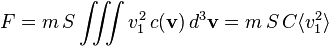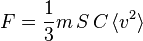Théorie cinétique des gaz - Définition
La liste des auteurs de cet article est disponible ici.
Vitesse et pression
Statistiques sur les vitesses
Considérons une molécule ayant une vitesse de norme v et frappant une surface. Elle subit un choc élastique, c'est-à-dire qu'elle repart en faisant un même angle avec la surface, avec une vitesse de même norme v. Si l'on choisit un repère orthonormé e, e, e, avec e perpendiculaire à la surface, alors cette vitesse se décompose selon les trois axes
On appelle c(v) d3v le nombre de molécules par unité de volume (la concentration) dont la vitesse est comprise dans un volume infinitésimal d3v autour de la valeur v. La concentration globale est donc :
La répartition statistique des vitesses étant isotrope, la moyenne des composantes de la vitesse est évidemment nulle :
Les moyennes quadratiques ne sont par contre pas nulles,et elles sont égales entre elles par symétrie de rotation. Comme on a toujours
(théorème de Pythagore), on a en moyenne
avec
et
Impact d'une molécule
Lorsqu'une molécule rebondit de manière élastique sur la surface, la composante perpendiculaire à la surface de sa quantité de mouvement varie de
m étant la masse de la molécule. D'après les lois de Newton (principe fondamental de la dynamique et théorème des actions réciproques), l'intégrale en temps de la force qu'elle imprime sur la surface est donc
Impact de toutes les molécules
On cherche maintenant, v étant fixé à d3v près, à savoir combien de molécules frappent une petite surface d'aire S durant une durée τ.
Les molécules frappant la surface entre l'instant 0 et l'instant τ sont nécessairement dans un cylindre de base S et de hauteur vτ — les autres molécules sont trop loin ou frappent à côté. Ce cylindre d'axe v a un volume de S v τ. La force d3F créée par toutes les molécules considérées est donc :
La force F créée par toutes les molécules s'obtient en intégrant sur v > 0 si l'on oriente e du gaz vers l'extérieur (on ne considère que les molécules allant vers la surface, pas celles s'en éloignant). Ceci revient à diviser par deux, en raison de la symétrie de la distribution c(v) :
En négligeant les fluctuations dans le temps de F, on peut intégrer sur t et simplifier par τ :
ou
La pression étant la force divisée par la surface, on obtient
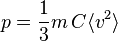
ou encore, par définition de C = n / V :