Théorie cinétique des gaz - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La théorie cinétique des gaz est une théorie par laquelle on cherche à expliquer le comportement macroscopique d'un gaz à partir des caractéristiques des mouvements des corpuscules qui le composent. Elle permet notamment de donner une interprétation microscopique aux notions de :
- température : c'est une mesure de l'agitation des corpuscules, plus précisément de leur énergie cinétique ;
- pression : la pression exercée par un gaz sur une paroi résulte des chocs des corpuscules sur cette dernière.
La théorie cinétique des gaz a été développée à partir du XVIIIe siècle et a été un des éléments déterminants dans la découverte de la notion d'atome. Elle est basée sur les idées de Daniel Bernoulli, John James Waterston, K.A. Krönig et Rudolf Clausius. James Clerk Maxwell et Ludwig Boltzmann en ont formalisé son expression mathématique.
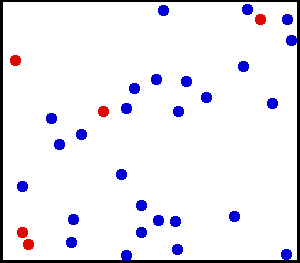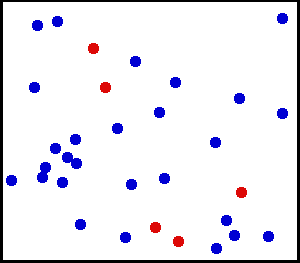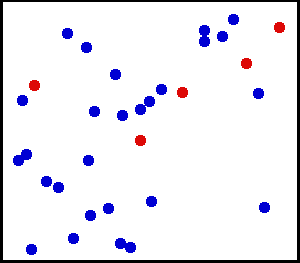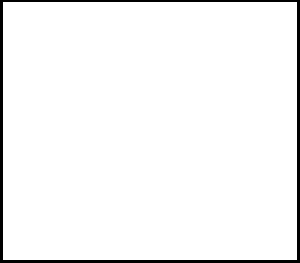
Selon les hypothèses retenues, la théorie peut être plus ou moins complexe et rendre compte de plusieurs phénomènes.
- Dans sa version la plus simple, on ignore les interactions entre les molécules, ainsi que leur taille. Elle permet de retrouver la loi des gaz parfaits.
- En prenant en compte les effets de taille des molécules, on peut décrire les collisions entre les molécules, ce qui donne accès aux propriétés de transport (viscosité, diffusion, effusion, conductibilité thermique).
- En introduisant de plus des interactions entre corpuscules, Van der Waals a proposé en 1873 une équation qui porte son nom et permet de décrire également la transition liquide-gaz (ébullition, évaporation, condensation). Elle a servi de guide à ceux qui, dans la seconde moitié du XIXe siècle, cherchaient à liquéfier tous les gaz, jusqu'à l'hélium, liquéfié en 1908 à Leyde.
Description
Un gaz est un ensemble de molécules mono- ou poly-atomiques subissant un certain nombre d’interactions : on aura notamment des interactions électromagnétiques (comme les forces de van der Waals) et des chocs entre les particules mais aussi contre les parois du récipient contenant le gaz. Dans le cadre de la théorie cinétique, on fait les approximations suivantes :
- le volume des molécules est négligeable
- seuls les chocs ont une influence, les autres interactions sont négligeables.
La trajectoire des molécules peut se modéliser avec le mouvement brownien.
- Approche intuitive du mouvement des molécules
Supposons que dans un récipient, toutes les molécules ont la même vitesse et la même direction. Ce système est instable parce que la moindre modification de trajectoire d'une seule molécule provoquera le heurt sur une autre molécule qui déviera et heurtera encore une autre avec un effet en chaîne qui établira le chaos donc le mouvement brownien.
- Dans la suite,
- P, désignera la pression du gaz,
- V, son volume,
- T, sa température thermodynamique, et
- n, le nombre de molécules.
Pression et énergie cinétique
Si une molécule de masse m se déplace à une vitesse v, son énergie cinétique vaut
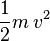
Gaz parfait monoatomique
Dans le cas d'un gaz parfait monoatomique, on suppose que la totalité de l'énergie est sous forme d'énergie cinétique des molécules (énergie thermique), donc l'énergie interne U du système vaut :
- U = Ec
On a donc
Gaz parfait de Laplace
Dans le cas plus général du gaz parfait de Laplace, on suppose que les molécules ont une énergie interne de rotation ou d'oscillation, proportionnelle à Ec. Le nombre de degrés de liberté passe de 3 à ν et dans l'hypothèse d'équipartition, on a
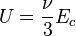
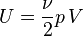
En modifiant adiabatiquement le volume du gaz, on fournit un travail − pdV égal à la variation d'énergie interne
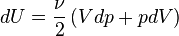
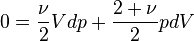
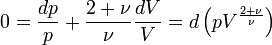
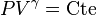
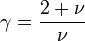
Pour le gaz parfait de Laplace, on a donc
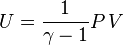
- Pour un gaz réel monoatomique, ou même l'hydrogène à très basse température ν = 3 et
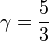
- Pour un gaz réel diatomique à température intermédiaire (azote, hydrogène, oxygène autour de 300 K), on a deux degrés de rotation possible
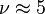
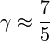
- Pour un gaz réel diatomique à très haute température, l'oscillation longitudinale devient possible, et ν tend vers 7 et γ tend vers