Théorie des modèles - Définition

Les modèles de la logique intuitionniste

Les modèles présentés jusqu'ici sont des modèles de la logique classique. Mais il existe d'autres logiques, par exemple la logique intuitionniste qui est une logique qui construit les démonstrations à partir des prémisses. Il existe pour cette logique une théorie des modèles, les modèles de Kripke avec un théorème de complétude : une formule est démontrable en logique intuitionniste si et seulement si elle est vraie dans tout modèle de Kripke.

Ces modèles permettent par exemple de répondre aux questions suivantes. Soit F une formule close :

• Ou bien F n'est pas un théorème de la logique intutionniste. Pour le montrer, il suffit d'exhiber un modèle de Kripke qui invalide la formule.
• Ou bien F est un théorème de la logique classique. Pour le montrer, il suffit d'en donner une démonstration dans un système de déduction de la logique classique. Il y a alors deux sous-cas :

Ou bien F est également un théorème de la logique intuitionniste. Pour le montrer, il suffit d'en donner une démonstration dans un système de déduction intuitionniste (ou de montrer que F est vraie dans tous les modèles de Kripke).

Ou bien F n'est pas démontrable en logique intuitionniste. Pour le montrer, il suffit de donner un modèle de Kripke invalidant la formule.

C'est ainsi qu'on peut démontrer que :

est un théorème de la logique classique, mais pas de la logique intuitionniste.

est un théorème de la logique intuitionniste (et également de la logique classique).

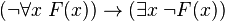
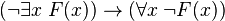
Les modèles de Kripke servent aussi à donner des modèles pour les logiques modales.

Voir également

• Calcul des prédicats
• Calcul des propositions
• Déduction naturelle
• Skolémisation
• Logique classique
• Logique intuitionniste
• Logique minimale
• Modèle
• Sémantique de Kripke