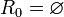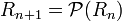Théorie des modèles - Définition

Les modèles du calcul propositionnel classique

En calcul propositionnel de la logique classique, il n'y a pas de quantificateurs existentiels ou universels. Les formules sont constituées de propositions atomiques reliées itérativement par des connecteurs logiques. Un modèle consiste à définir, pour chaque variable propositionnelle atomique, une valeur de vérité (vraie ou fausse). On peut alors en déduire la vérité ou la fausseté de toute formule complexe.

La complexité d'une formule est mesurée par le nombre maximal d’opérateurs emboîtés. Par exemple dans , le ou et le non sont emboîtés l’un dans l’autre. Mais le non et le et ne le sont pas. Cette proposition est de complexité 2 parce qu’elle a au maximum deux opérateurs emboîtés.

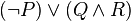
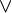
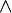
Les formules de complexité 0 sont les formules atomiques. C'est le modèle choisi qui définit leur valeur de vérité.

Supposons que la vérité et la fausseté de toutes les formules de complexité n ait été définie. Montrons comment définir la vérité et la fausseté des formules de complexité n + 1. Soit P une formule de complexité n + 1, obtenue à partir de la formule ou des formules Q et R de complexité n ou inférieure, au moyen d'un connecteur logique. La vérité ou la fausseté de Q et R est donc déjà définie.

a)  : Si Q est vrai alors P est faux, par définition de la négation. Si Q est faux alors P est vrai, pour la même raison.

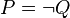
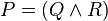
b)  : Si Q et R sont tous les deux vrais alors P aussi, mais P est faux dans tous les autres cas.

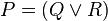
c)  : Si Q et R sont tous les deux faux alors P aussi, mais P est vrai dans tous les autres cas.

d)  : Si Q est vrai et R est faux alors P est faux, mais P est vrai dans tous les autres cas.

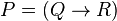
Une formule vraie dans tout modèle s'appelle une tautologie. Si la formule possède n variables propositionnelles atomiques, il suffit en fait de vérifier la vérité de la formule dans les 2ⁿ modèles possibles donnant les diverses valeurs de vérité aux n propositions atomiques. Le nombre de modèles étant fini, il en résulte que le calcul des propositions est décidable : il existe un algorithme permettant de décider si une formule est une tautologie ou non.

Par ailleurs, le théorème de complétude du calcul des propositions établit l'équivalence entre être une tautologie et être prouvable dans un système de déduction adéquat.

Exemples

Montrons que (loi de Peirce) est une tautologie, en utilisant la règle d). Si P est vraie, alors étant de la forme est vraie. Si P est faux, alors est vrai, est faux, et est vrai.

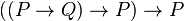
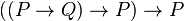
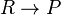
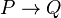
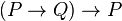
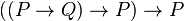
Étant vrai dans tout modèle, est une tautologie. Elle est donc également prouvable au moyen de systèmes de déduction, par exemple la déduction naturelle.

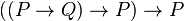
Par contre, n'est pas prouvable. En effet, dans un modèle où P est faux, est également faux.

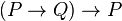
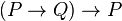
Exemples d'application des modèles

Nous avons déjà donné des applications des modèles :

• satisfaire ou au contraire falsifier une formule (par exemple distinguer formule vraie en logique classique mais fausse en logique intuitionniste : la formule est vraie dans tout modèle classique, mais il existe un modèle en logique intuitionniste qui la falsifie).
• prouver qu'une théorie ou un système d'axiomes n'est pas contradictoire en exhibant un modèle satisfaisant tous les axiomes.

En ce qui concerne les systèmes d'axiomes, les modèles interviennent également pour montrer l'indépendance des axiomes entre eux, ou établir la non-contradiction d'un système axiomatique en s'appuyant sur la non-contradiction d'un autre système (on parle alors de « consistance relative » ). Donnons quelques exemples.

En géométrie, le V^e postulat d'Euclide est indépendant des autres axiomes de la géométrie. En effet, d'une part, le plan de la géométrie euclidienne est un modèle dans lequel ce postulat est vrai. D'autre part, le demi-plan de Poincaré est un modèle de la géométrie hyperbolique dans lequel ce postulat est faux. Dans ce modèle, l'univers (le plan hyperbolique) est constitué des points du demi-plan euclidien ouvert supérieur . Les droites du plan hyperbolique sont les ensembles d'équation x = a ou (x − a)² + y² = R².

Dans cet univers, si on se donne une droite et un point extérieur à cette droite, il existe une infinité de droites passant par le point et non sécantes à la première droite.

Dans cet exemple, on voit qu'on peut construire un modèle de la nouvelle théorie (le plan hyperbolique et ses droites) en se servant d'un modèle de l'ancienne (dans le plan euclidien : le demi-plan et ses demi-droites et demi-cercles). Si on suppose la « cohérence » ou « consistance » de la géométrie euclidienne, alors on a établi celle de la géométrie hyperbolique.

Cette utilisation de modèles pour montrer la consistance relative d'une théorie est très fréquente. Considérons par exemple la théorie des ensembles, notée ZF. Considérons par ailleurs la théorie, notée ZFC, constituée de ZF à laquelle on ajoute l'axiome du choix. On peut montrer que si ZF est non contradictoire alors ZFC aussi. En effet (grâce au théorème de complétude de Gödel) on suppose qu'il existe un modèle de ZF. On est alors capable, dans ce modèle, d'associer à tout ordinal α un ensemble F_α de façon que :

• la classe L "réunion" de tous les F_α vérifie tous les axiomes de ZF,
• les F_α sont constructibles par récurrence transfinie, dans le sens où F_α est défini à partir des F_β, pour β < α
• si l'on définit l'ordre d'un y de L comme étant le plus petit ordinal α tel que y appartienne à F_α, alors, à tout x non vide de L "on peut associer" un élément de x d'ordre minimal, que l'on note f(x).

On a alors défini une "fonction" f de L dans L (ou plus exactement, une classe fonctionnelle) vérifiant . Autrement dit, f est une "fonction de choix" dans L, si bien que L vérifie non seulement ZF mais aussi l'axiome du choix. L est donc un modèle de ZFC.

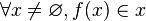
Toujours dans un modèle de ZF, si l'on pose et pour tout entier n, (ensemble des parties de R_n), alors la réunion des R_n pour tout n entier définit un modèle qui vérifie tous les axiomes de ZF sauf l'axiome de l'infini. Ceci prouve (toujours sous l'hypothèse que ZF est non contradictoire) que ce dernier axiome ne peut être dérivé des autres axiomes.