Nombre de Catalan - Définition

Les nombres de Catalan sont des entiers naturels qui se rencontrent souvent dans les problèmes de combinatoire. Ils forment une suite dont le terme d'indice n, appelé nème nombre de Catalan est défini par

(voir coefficient binomial). Les premiers nombres de Catalan pour n=0, 1, 2, 3, ... sont

1, 1, 2, 5, 14, 42, 132, 429, 1430, ...

Tous les nombres de Catalan sont des entiers naturels parce qu'ils peuvent s'écrire sous la forme:

pour n≥1,

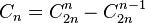
Applications en combinatoire

• C_n est égal au nombre de mots de Dyck de longueur 2n. Un mot de Dyck est un mot formé de n lettres X et de n lettres Y, tel qu'aucun abrègement du mot à la finale (obtenu en supprimant les dernières lettres à partir d'un rang quelconque) ne contienne plus de Y que de X. Autrement dit, lorsque nous parcourons un mot de Dyck de gauche à droite, le nombre de X rencontrés est toujours supérieur ou égal au nombre de Y. Par exemple, les mots de Dyck de la longueur 6 sont:

XXXYYY, XYXXYY, XYXYXY, XXYYXY, XXYXYY.

En l'occurrence, C₃= 5.
Assimilant X à une parenthèse ouvrante et Y à une parenthèse fermante, un mot de Dyck de longueur 2n peut être vu comme une expression formée de n paires de parenthèses correctement assemblées: ((())), ()(()), ()()(), (())(), (()()). Les mots de Dyck peuvent être naturellement représentés comme des chemins dans un quadrillage de n +1 points par n+1 points, reliant certains points par les traits verticaux et horizontaux. Ces chemins commencent dans le coin inférieur gauche, et se terminent dans le coin supérieur droit, en allant toujours vers le haut ou vers la droite, mais ne passant jamais au-dessus de la diagonale principale. X représente alors un " déplacement vers la droite " et Y représente un " déplacement vers le haut ".
Nous pouvons compter les mots de Dyck avec l'astuce suivante due à D. André (principe de symétrie): intéressons nous aux mots contenant n X et n Y qui ne sont pas des mots de Dyck. Dans de tels mots, déterminons le premier Y qui brise la condition de Dyck, puis modifions toutes les lettres qui suivent ce Y, en échangeant X avec Y et vice versa. Nous obtenons un mot avec n + 1 Y et n- 1 X, et en fait tous les mots comportant n + 1 Y et n- 1 X peuvent être obtenus par ce moyen et de manière unique. Le nombre de ces mots est le nombre de façons de placer les n-1 X dans 2n emplacements et est égal à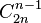

ce qui donne le nombre de mots qui ne sont pas de Dyck; le nombre de mots de Dyck s'en déduit et est égal à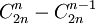

qui est le nème nombre de Catalan C_n.

• C_n est également le nombre de façons différentes de placer des parenthèses autour de n + l facteurs. Pour n = 3 par exemple, nous obtenons 5 façons différentes de placer des parenthèses autour de 4 facteurs: a(b(cd)), a((bc)d), (ab)(cd), (a(bc))d, ((ab)c)d. De telles expressions peuvent être naturellement représentées par des arbres binaires complets ordonnés, et C_n donne également le nombre de ces arbres à n + 1 feuilles.

Triangulations

• C_n est également égal au nombre de différentes façons dont un polygone à n + 2 côtés peut être partagé en triangles en reliant ses sommets par des segments de droite.
• C_n est également le nombre de partitions non croisées de l'ensemble {1, ..., n }. A fortiori, C_n n'excède jamais le nème nombre de Bell.

Relation de récurrence et comportement asymptotique

Les nombres de Catalan satisfont la relation de récurrence

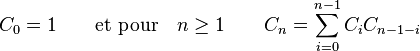
Ceci vient du fait que tout mot w de Dyck de longueur supérieure à 2 peut s'écrire de manière unique sous la forme

w = Xw₁Yw₂
avec des mots de Dyck (éventuellement vides) w₁ et w₂.

La fonction génératrice des nombres de Catalan est définie par

et en utilisant la relation de récurrence ci-dessus nous voyons que

et par conséquent

Asymptotiquement, les nombres de Catalan se comportent comme

Histoire

La suite de Catalan fut décrite pour la première fois au XVIII^e siècle par Leonhard Euler, qui s'était intéressé au nombre de différentes façons de partager un polygone en triangles. La première publication sur ces nombres est due à Segner et la suite porte alors le nom de Nombre de Segner. Eugène Charles Catalan fit le lien avec le nombre d'expressions " parenthésées " et le nom de Catalan remplaça celui de Segner. L'astuce de comptage des mots de Dyck fut trouvée par Désiré André en 1887.