Démonstration du théorème de Fermat - Définition
Enoncé
On rappelle que le théorème de Fermat s'énonce ainsi :
Un entier premier impair n est la somme de deux carrés entiers si et seulement s'il est congru à 1 modulo 4.
Démonstration
Elle s'appuie sur deux lemmes :
Lemme 1
Si n est un entier premier impair, le groupe Z/nZ* contient exactement (n-1)/2 carrés, et ce sont les racines du polynôme
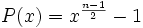
Preuve
Le morphisme du groupe multiplicatif (Z/nZ)* qui a x associe x² a pour image l'ensemble des carrés et pour noyau {1, -1}. Il existe donc une bijection entre l'ensemble des carrés et (Z/nZ)*/{1, -1}, dont le cardinal est (n-1)/2.
En outre, si x = y² est un carré, par le petit théorème de Fermat, nous avons
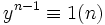
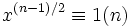
Lemme 2
Il s'énonce ainsi : Pour tout réel ξ et tout réel H > 1, il existe un couple (p, q) d'entiers tels que q < H et |qξ - p| ≤ 1/H
Preuve
Supposons H entier. Les H+1 réels {0, ξ - [ξ], 2ξ - [2ξ], 3ξ - [3ξ]…, 1} où [α] désigne la partie entière de α sont tous compris entre 0 et 1. Donc au moins deux d'entre-eux ont une distance inférieure à 1/H. Si ces deux réels sont iξ - [iξ] et i'ξ - [i'ξ] avec i < i', alors q = i' - i et p = [i'ξ] - [iξ] donne :
0 < q < H et |qξ - p| = |i'ξ - iξ - [i'ξ] + [iξ]| ≤ 1/H.
On vérifie que l'inégalité est également vraie si l'un des deux réels est égal à 1.
Si H n'est pas entier, on applique le raisonnement sur [H] + 1. Comme q est entier, q < [H] + 1 implique q < H, CQFD.
Raisonnement
Condition nécessaire
Si n est un nombre impair somme de deux carrés, alors nécessairement ces carrés sont de parité différente. Le carré pair est nécessairement multiple de 4, donc congru à 0 modulo 4. L'autre carré est le produit d'un nombre congru à 1 ou 3 modulo 4, donc son carré est nécessairement congru à 1 modulo 4.
Condition suffisante
Si n est congru à 1 modulo 4, l'égalité ( − 1)(n − 1) / 2 = 1 montre d'après le lemme 1 que -1 est un carré et donc qu'il existe un m tel que
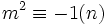
Appliquons maintenant le lemme 2 avec ξ = m/n et H = √n. Il existe (p,q) tel que q < √n et |qm/n - p| ≤ 1/√n.
Posons r = qm - pn. Alors |r| ≤ √n, donc q² + r² < 2n.
En outre, q² + r² est congru à q² + q²m² = q(m² + 1) = 0 modulo n. Comme q² + r² < 2n, q² + r² = n, CQFD.

















































