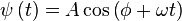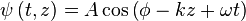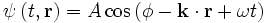Vecteur d'onde - Définition et Explications

En physique, un vecteur d'onde (ou " vecteur de phase ", en électronique notamment) est comme son nom l'indique un vecteur représentant une onde. La norme du vecteur correspond au nombre d'onde (lié à l'inverse de la longueur d'onde), et sa direction indique la direction de propagation de l'onde (Une onde est la propagation d'une perturbation produisant sur son passage une variation réversible...).

Le vecteur (En mathématiques, un vecteur est un élément d'un espace vectoriel, ce qui permet...) d'onde (Une onde est la propagation d'une perturbation produisant sur son passage une variation...) est très utile pour généraliser l'équation (En mathématiques, une équation est une égalité qui lie différentes quantités, généralement...) d'une onde à la description d'une famille d'ondes. Si toutes les ondes d'une famille se propagent dans la même direction et possèdent la même longueur (La longueur d’un objet est la distance entre ses deux extrémités les plus...) d'onde, elles peuvent toutes être décrites par le même vecteur d'onde. Le cas le plus courant d'une famille d'onde respectant ces conditions est celle d'une onde plane (L'onde plane est un concept issu de la physique de la propagation des ondes. C'est une onde dont...), pour laquelle la famille d'ondes est également cohérente (toutes les ondes possèdent la même phase).

Par exemple, une représentation courante d'une onde en un point (Graphie) de l'espace est :

• A est l'amplitude (Dans cette simple équation d’onde :) de l'onde.
• ω est la fréquence angulaire (En physique, et plus spécifiquement en mécanique, la vitesse angulaire ω, aussi appelée...) ou pulsation.
• φ est le déphasage de l'onde.
• t est la variable (En mathématiques et en logique, une variable est représentée par un symbole. Elle...) temps (Le temps est un concept développé par l'être humain pour appréhender le...).

Pour généraliser cette équation à tous les points d'un espace unidimensionnel dans la direction de propagation, il est nécessaire d'ajouter un second terme de déphasage :

• k est le nombre (La notion de nombre en linguistique est traitée à l’article « Nombre...) d'onde.
• z est la variable d'espace dans la direction de propagation.

Dans le cas d'un espace à trois dimensions (Dans le sens commun, la notion de dimension renvoie à la taille ; les dimensions d'une pièce...) et dans le cas d'onde planes, il est aisé de généraliser la formule précédente en remplaçant le nombre d'onde k par le vecteur d'onde :, et la variable d'espace z par le vecteur position ::

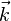
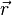
Le raisonnement est similaire pour des ondes "non planes", mais avec une amplitude A dépendant de la position.