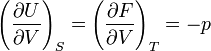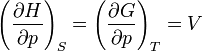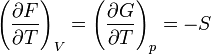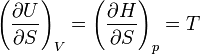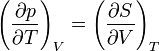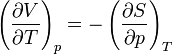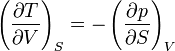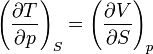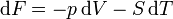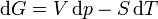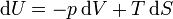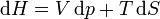Relations de Maxwell - Définition
On appelle relations de Maxwell ou encore " équations de Maxwell " en thermodynamique, l'ensemble des quatre équations suivantes :
on trouve aussi:
Pour démontrer ces équations, il suffit d'appliquer le théorème de Schwarz aux formes différentielles exactes suivantes :
Une application : première loi de Joule
Pour un gaz parfait, on a donc d'après ce qui précède
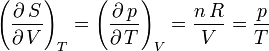
D'autre part,
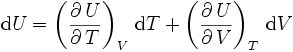
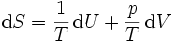
On en déduit
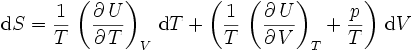
Ainsi,
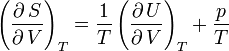
d'où, d'après ce qui précède,
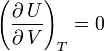
l'énergie interne d'un gaz parfait ne dépend que de sa température.
En effectuant ces calculs pour un gaz de Van der Waals, c.-à-d. un gaz dont l'équation d'état est
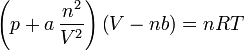
on trouve
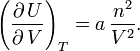
Notons que cette méthode ne permet pas d'expliciter la dépendance de U en T : en effet, on sait par ailleurs qu'elle fait intervenir le coefficient de Laplace γ qui n'apparaît ni dans les identités thermodynamiques ni dans l'équation d'état.
Notations utilisées dans cet article
- V : Volume
- p : Pression
- T : Température
- U : Énergie interne
- H : Enthalpie
- F : Énergie libre
- G : Enthalpie libre
- S : Entropie
- R : Constante des gaz parfaits
- a et b : paramètres de l'équation de Van der Waals