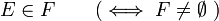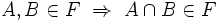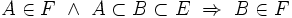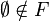Filtre (mathématiques) - Définition
Definition générale
En mathématiques, un filtre est une partie F non vide d'un ensemble partiellement ordonné (P,≤) vérifiant les deux conditions suivantes:
- Pour tout x, y dans F, il existe z dans F, tel que z ≤ x et z ≤ y. (C'est une base de filtre.)
- Pour tout x dans F et y dans P, x ≤ y implique que y est dans F.
Le filtre F est propre ssi il n'est pas égal à P en entier.
Cas particuliers
Filtre sur un ensemble
Un cas important est celui où P=P(E) est l'ensemble des parties d'un ensemble E, ordonné par l'inclusion:
Définition
F est un filtre sur E ssi
Les filtres sont la structure naturelle pour définir la notion de convergence en topologie.
Exemple
L'ensemble de toutes les parties de E contenant une partie non vide donnée A de E (en particulier, un singleton A={x}), forme un filtre sur E, appelé filtre principal engendré par A.
Le filtre de Fréchet sur un ensemble infini E est l'ensemble des parties de E ayant un complément fini dans E.
Un ultrafiltre est un filtre égal à sa grille.
Base de filtre
Si B est une partie de P(E) ne contenant pas l'ensemble vide et telle que toute intersection finie contient un élément de B non vide, il existe un unique filtre minimal F contenant B, appelé filtre engendré par B.
Si B contient toute intersection finie de ses éléments, alors F est égal à l'ensemble des sur-ensembles des éléments de B, et B est une base de filtre pour F.
C'est la structure élémentaire pour définir des limites : Une fonction (en particulier une suite) f à valeurs dans un espace topologique E admet L comme limite suivant la base de filtre B, ssi pour tout voisinage V de L, il existe A dans B, tel que la restriction de f à A soit à valeurs (c-à-d. f(A) soit inclu) dans V.