Genre (mathématiques) - Définition
Topologie
Surface close
Le genre d'une courbe algébrique, c'est-à-dire d'une surface (i.e. un espace topologique dont tout point possède un voisinage homéomorphe au plan) connexe, est le nombre maximum de courbes fermées simples sans points communs pouvant être tracées à l'intérieur de cette surface sans la déconnecter. Autrement dit, dans le procédé de détermination du genre, le complément de ces courbes reste connexe.
Plus concrètement, si l'on considère que la surface est en papier, le genre est le nombre maximal de découpages fermés faisables sans que la surface ne soit séparée en plusieurs morceaux.
C'est une notion de topologie : deux surfaces n'ayant pas le même genre ne sont pas homéomorphes.
Exemples
Courbe non-singulière
Le genre d'une courbe non-singulière dans l'espace projectif
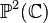
Exemples
- Une courbe elliptique a un genre de 1.
Théorie des nœuds
Le genre d'un nœud est la moitié du nombre minimal d'anses qu'il est nécessaire d'ajouter à la sphère afin de pouvoir tracer une ligne de découpe à sa surface avec le nœud, afin que celle-ci se divise en deux lors de la découpe.
Exemples
- Un nœud de trèfle est de genre 1.
- Un nœud trivial est de genre 0.
Théorie des graphes
Le genre d'un graphe est le plus petit entier p pour que le graphe soit représentable sur une surface orientable de genre p.
Exemples
- Les graphes planaires sont de genre 0.
- Le graphe des puits des trois maisons est de genre 1.

















































