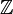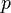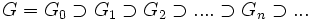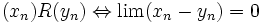Groupe topologique - Définition
On appelle groupe topologique tout groupe (G,*) muni d'une topologie satisfaisant aux conditions suivantes:
- L'application (
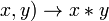
- L'application
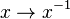
Exemples de base
- Le groupe additif
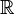
On peut montrer qu'un sous-groupe de
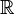
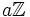
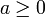
- Le cercle
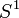
multiplicatif des nombres complexes de module
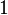
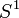
- Un exemple plus sophistiqué est
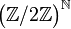
Ce groupe est homéomorphe à l'ensemble de Cantor. Pour le voir, on a besoin de la notion de produit infini d'espaces topologiques.
Quelques propriétés générales
- Dans un groupe topologique, les translations
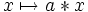
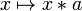
- La topologie est déterminée par
la donnée des voisinages de l'élément neutre.
- Un groupe topologique est séparé si et seulement si
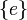

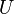
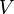
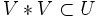
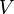
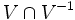
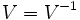
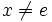
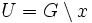
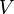
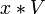


- Si
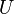
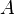


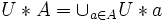
Dorénavant, nous omettrons le signe

Groupes linéaires
Une classe importante de groupes topoloqiques est formée par les sous-groupes du groupe linéaire
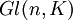
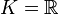

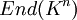
Ces exemples sont des exemples fondamentaux de groupes de Lie réels ou complexes.
Ils ont en commun la propriété suivant : il existe un ouvert contenant l'élement neutre et ne contenant aucun sous-groupe non trivial.
Topologie p-adique
Si (G,+) est un groupe abélien, si (Gn) est une suite de sous-groupes de G telle que:
Alors la suite (Gn) induit une topologie sur G dans laquelle les voisinages de x sont les ensembles x+ Gn.
Si de plus, l'intersection des Gn est réduite à {0} où 0 est l'élément neutre de G, le groupe est séparé.
Un cas particulier de groupe topologique de cette forme est le groupe muni de la topologie p-adique: Si p est un entier naturel, la suite (Gn) est définie par Gn = pnG . (on rappelle que, pour tout entier naturel k et tout élément x de G, l'élément kx est défini par kx = x + x + ... + x (où x apparait k fois)
Distance induite
On peut définir une distance sur (G, +) muni de la topologie induite par (Gn) si l'intersection des Gn est bien réduite à {0}:
-
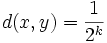
- d(x,y) = 0 si pour tout entier k,
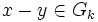
Complété
Si (G,+) est un groupe abélien séparé muni de la topologie déterminée par la suite (Gn), on peut définir dans G des suites de Cauchy
- (xn) est de Cauchy si et seulement si, pour tout voisinage V(0) de 0, il existe un entier n tel que
- pour tout
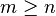
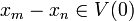
- pour tout
Sur cet ensemble de suites SC(G), on peut définir une relation d'équivalence :
L'ensemble quotient SC(G) est alors espace complet.
Le groupe G est alors isomorphe à un sous-groupe dense de SC(G).
L'exemple le plus important d'une telle construction est celui des nombres p-adiques : on fait cette construction à partir de