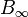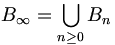Théorie des tresses - Définition
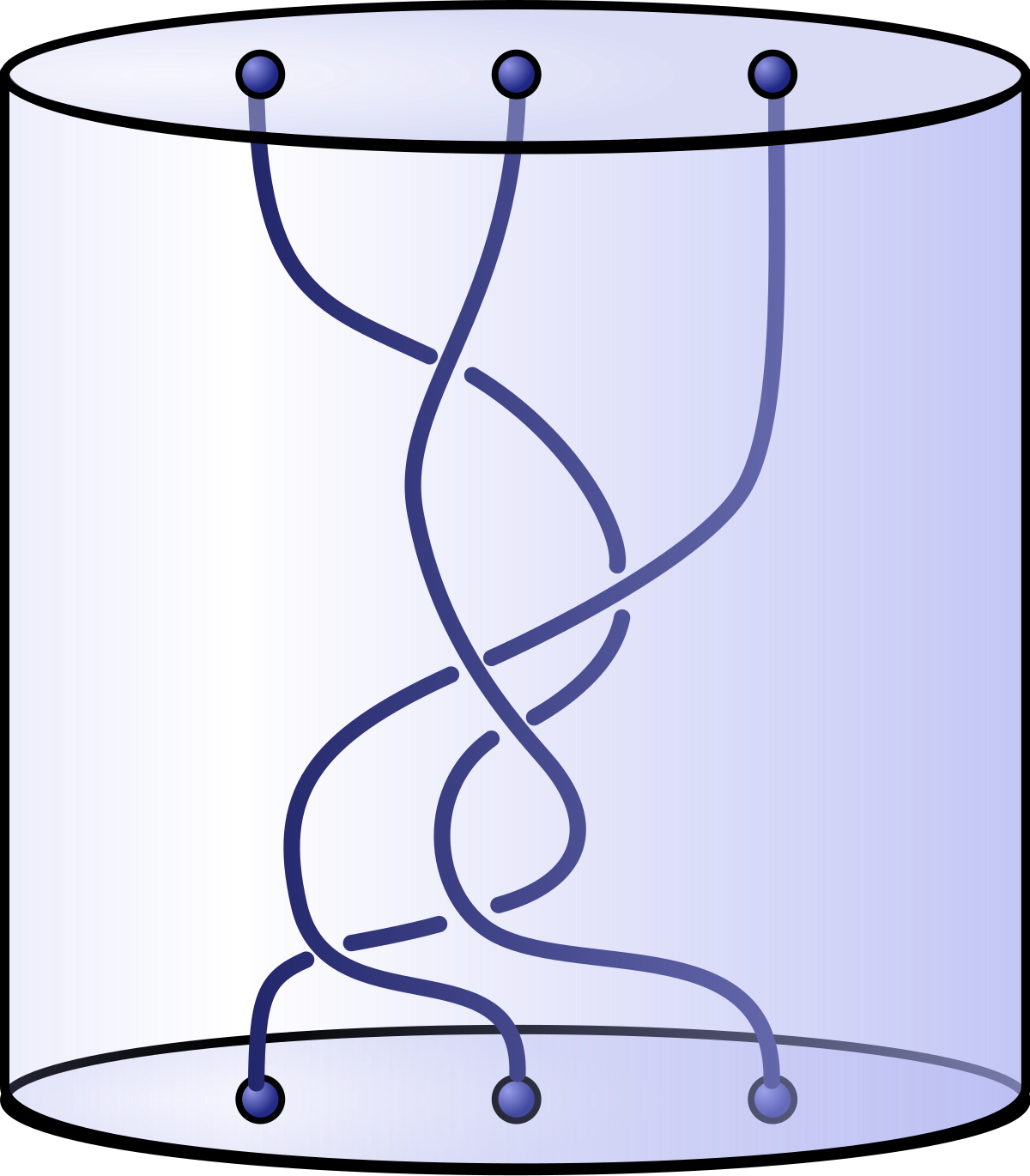
La théorie des tresses est l'étude des tresses, objet mathématique formalisant ce qu'on appelle tresse dans la vie courante.
Définition
Soit
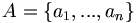
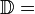

On appelle brin le graphe d'une application b continue de
![I=\left[0,1\right]](https://static.techno-science.net/illustration/Definitions/autres/c/c4f212a520e6f2ca5485d0cadc5d7db4_4b6f23bc2502a1659ebf66052ba7383b.png)

On appelle tresse à n brins la réunion de n brins disjoints.
Reformulation
Géométriquement on projette la représentation 3D d'une tresse dans le plan. On obtient ainsi un diagramme de tresse. Afin de ne pas perdre d'information vis-à-vis de l'espace en 3 dimensions il faut indiquer, lorsque deux brins se croisent, lequel passe devant l'autre.
L'ordre d'arrivée des brins est différent de l'ordre départ. Les positions ont subi une transformation ; ici il s'agit de la permutation de (1 4 3). L'étude des tresses est liée à l'étude des permutations et offre une donnée supplémentaire en ajoutant une idée de chemin (ordre des opérations effectuées dans la transformation) inexistante dans les permutations. À chaque diagramme de tresses de n brins on associe une permutation de
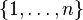
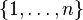
Ceci nous amène à introduire une tresse particulière, la tresse triviale où aucun croisement n'a lieu entre les différents brins. Par exemple, voici le diagramme de la tresse triviale à quatre brins.
On veut munir l'ensemble des diagrammes de tresse d'une structure mathématique. Notons tout d'abord que la longueur des brins importe peu dans la structure de la tresse ; elle est totalement caractérisée par les croisements des brins et l'ordre dans lequel ces croisements sont effectués. Ainsi même s'ils n'ont pas la même longueur, deux diagrammes de tresse qui ont les mêmes croisements dans le même ordre sont considérés comme égaux.
Cela nous permet de munir l'ensemble des diagrammes de tresse d'une structure de monoïde, de la façon suivante :
On définit le produit de deux diagrammes de tresse ayant le même nombre de brins n en opérant une concaténation, i.e. en accrochant le second à la fin du premier ce qui donne un nouveau diagramme de tresse à n brins :
Ce produit est associatif mais non commutatif. On remarque de plus que le produit d'un diagramme de tresse β et du diagramme de la tresse triviale donne un diagramme de tresse identique au diagramme β. Ainsi le diagramme trivial est un élément neutre pour la concaténation.
L'ensemble des diagrammes de tresse à n brins muni de la concaténation est donc un monoïde. Notons le Tn.
Remarque
Pour que les diagrammes de tresses et leur produit correspondent aux permutations et leur composition il faut lire les diagrammes de tresses de bas en haut. Par exemple, le diagramme de tresses suivant a pour permutation (143).
Ainsi prenons deux diagrammes de tresses b1 et b2 de permutation associée respective s1 et s2. Le produit b1b2 a pour permutation
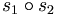
Pour étudier les tresses, il faut les comparer vis-à-vis de leur chemin et de leur permutation associée. Dans un diagramme de tresses, certains croisements sont indépendants les uns des autres.
Deux diagrammes de tresses sont dits 'isotopes' si on peut obtenir l'un à partir de l'autre en déplaçant les brins sans les " couper " et sans toucher aux extrémités.
La relation d'isotopie sur Tn est une relation d'équivalence.
Notons que deux diagrammes de tresses isotopes représentent la même permutation, mais la réciproque est fausse : deux diagrammes ayant la même permutation associée ne sont pas nécessairement isotopes.
Groupe de tresses à n brins
En quotientant Tn par la relation d'isotopie on obtient une structure de groupe sur l'ensemble des diagrammes de tresses à n brins. On note Bn et on appelle 'groupe de tresse à n brins' le groupe ainsi obtenu. L'élément neutre étant bien évidemment la classe du diagramme trivial, l'inverse d'un diagramme est le diagramme obtenu en prenant son image miroir.
Image:TresseInv.ps
Par simplification on appelle tresse à n brins un élément de Bn.
Groupe de tresses
On plonge Bn dans Bn + 1 en transformant les tresses à n brins en tresses à n + 1 brins de la manière suivante. On ajoute à droite un n + 1ème brins qui n'en croise aucun autre, comme on le voit dans l'exemple suivant:
On note