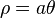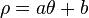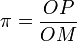Spirale d'Archimède - Définition
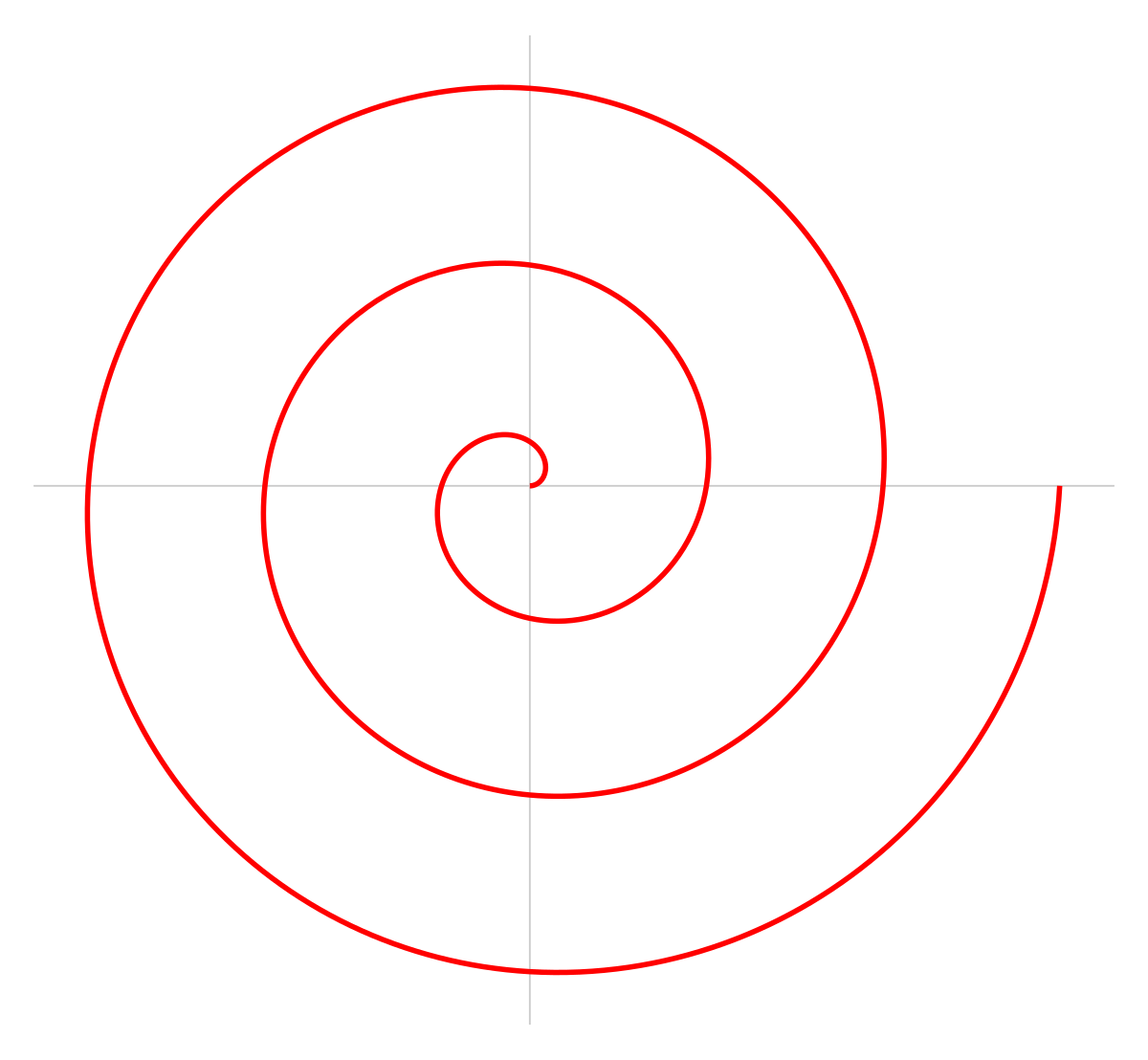
La spirale d'Archimède est la courbe d'équation polaire suivante :
La spirale d'Archimède est la courbe décrite par un point en déplacement uniforme sur une droite en rotation elle-même uniforme autour d'un point. Le sillon des disques vinyles est une spirale d'Archimède.
La spirale dessinée ci-contre est une spirale définie pour des angles positifs. La spirale d'équation r = − t / π définie pour des angles négatifs serait l'image de la précédente par une symétrie d'axe (Ox). Bref, elle aurait la même forme mais tournerait dans l'autre sens.
La courbe d'équation polaire :
est aussi une spirale d'Archimède. C'est la spirale précédente ayant subi une rotation d'angle -b/a.
Construction mécanique
On peut envisager une construction mécanique d'une spirale d'Archimède en posant la feuille de papier sur un socle muni d'un mouvement de rotation uniforme autour d'un axe vertical passant par O. Le crayon, lui, s'éloigne du centre O suivant un mouvement rectiligne uniforme. Les deux mouvements peuvent être liés par un système de vis sans fin.
Loi des aires
L'aire balayée par un rayon sur l'intervalle [0;θ] est
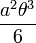
Attention, cela ne correspond pas à l'aire de la spirale car le rayon risque de balayer plusieurs fois la même portion de plan.
Problèmes célèbres
Trisection de l'angle
Une spirale d'Archimède permet de résoudre le problème de la trisection de l'angle : pour un angle θ donné, il est possible de construire à la règle et au compas l'angle θ / 3. Il suffit de repérer le point M de la spirale associé à l'angle θ, de construire un cercle de centre O et de rayon OM/3. Ce cercle coupe la spirale en un point P associé à l'angle θ / 3.
Rectification du cercle
La rectification du cercle est une problème analogue à sa quadrature. Chercher la quadrature du cercle, c'est chercher le carré qui a la même aire qu'un cercle donné. Chercher la rectification du cercle c'est chercher une segment de droite qui a même longueur que le périmètre du cercle. Dans l'un des cas (la quadrature) il s'agit de représenter
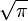
On utilise la propriété de la tangente à la spirale au point M associé à l'angle θ. On peut démontrer que l'angle α que fait cette tangente avec la droite (OM) n'est pas constant, comme c'est le cas dans une spirale logarithmique, mais varie en fonction de θ selon la loi suivante :
-
-
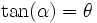
-
Il suffit alors de tracer la tangente à la spirale au point M associé à π. Elle rencontre la droite (Oy) en P. On obtient alors le rapport
Problèmes non résolus
Les deux paragraphes précédents pourraient laisser croire qu'Archimède, grâce à sa spirale, aurait résolu les deux problèmes classiques de la trisection de l'angle et de la quadrature du cercle. Mais il n'en est rien. Les mathématiciens de l'époque cherchaient des méthodes de résolutions à la règle et au compas et méprisaient les résolutions mécaniques. C'est pourquoi la spirale d'Archimède n'a pas été considérée comme un outil de résolution et a été rejetée comme l'ont été d'autres quadratrices et d'autres trisectrices.
Il est à noter de plus que le tracé de la tangente à la spirale ne faisait que déplacer le problème.