Axiome de l'infini - Définition
En théorie axiomatique des ensembles et dans les branches de la logique, des mathématiques, et de l'informatique, l'axiome de l'infini est l'un des axiomes de la théorie des ensembles de Zermelo-Fraenkel. Il énonce qu'il existe un ensemble infini.
Dans le langage formel de l'axiomatique de Zermelo-Fraenkel, l'axiome s'écrit:
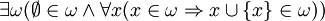
ou en d'autres termes: il existe un ensemble ω; tel que l'ensemble vide
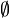
Pour comprendre cet axiome, appelons tout d'abord
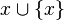
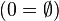
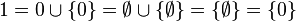
De même, 2 est le successeur de 1:
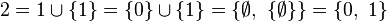
et ainsi de suite. Une conséquence de cette définition est que chaque nombre entier est égal à l'ensemble de tous les nombres entiers qui le précèdent. Nous pourrions envisager de former, en utilisant ce procédé, l'ensemble de tous les nombres entiers naturels; mais il s'avère qu'en utilisant seulement ces axiomes la construction est impossible. L'axiome de l'infini assure l'existence de cet ensemble ω et il le définit par une méthode semblable à celle du raisonnement par récurrence, en supposant d'abord que ω contient zéro, puis en imposant que le successeur d'un quelconque élément de ω soit également dans ω.
Cet ensemble peut contenir d'autres éléments que les nombres entiers naturels (qui forment un sous-ensemble de ce premier), mais nous pouvons appliquer le schéma d'axiomes de compréhension pour retirer les éléments indésirables, libérant l'ensemble ω de tous les nombres entiers naturels. Cet ensemble est unique d'après l'axiome d'extensionnalité. Ainsi l'axiome affirme essentiellement que:
- Il existe un ensemble contenant tous les nombres entiers naturels.
L'axiome de l'infini est également l'un des axiomes de von Neumann-Bernays-Gödel.

















































