Conjecture abc - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

La conjecture abc est une des conjectures les plus étudiées en théorie des nombres. Elle a été formulée pour la première fois par Joseph Oesterlé et David Masser en 1985. Si elle était vérifiée, elle permettrait comme nous allons le voir de démontrer aisément le théorème de Fermat entre autres.

Formulation

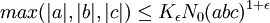
Soit $ε > 0$ , alors il existe une constante $K ε$ telle que, pour tous $a, b, c$ entiers relatifs premiers entre eux vérifiant $a + b = c$ , on ait: $max(|a|,|b|,|c|)\le K_\epsilon N_0(abc)^{1+\epsilon}$

où $N 0 (n)$ est le radical de n, c'est-à-dire le produit des nombres premiers divisant n.

Analogie avec les polynômes

L'idée de la conjecture abc s'est formée par analogie avec les polynômes. Un théorème abc est en effet disponible pour les polynômes sur un corps algébriquement clos de caractéristique nulle. Il est aussi appelé théorème de Mason-Stothers et se formule ainsi:

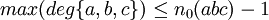
Pour tous $a, b, c$ polynomes premiers entre eux vérifiant $a + b = c$ , on a: $max(deg\{a,b,c\})\le n_0(abc)-1$

où $n 0 (P)$ est le nombre de racines distinctes de P.

Ce théorème permet de démontrer de manière aisée le théorème de Fermat pour les polynomes: l'équation $x n + y n = z n$ , x, y et z non constants n'a pas de solutions si $n\ge 3$ .

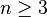
La tentation est alors grande de trouver un analogue pour les entiers, car il permettrait de démontrer tout aussi facilement le théorème de Fermat.

Une des principales conséquences: le théorème de Fermat

En fait, la conjecture abc ne permettrait pas exactement de montrer le théorème de Fermat, mais une version asymptotique dans le sens où on montre qu'il existe N tel que pour tout $n\ge N$ , $x n + y n = z n$ n'a plus de solutions entières. Ce N serait cependant explicite car comme nous allons le voir dépendant du $C ε$ , explicitement donné par la démonstration du théorème abc.

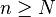
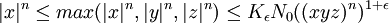
En prenant un $ε$ quelconque (ou 1 pour fixer les idées), lorsque $x n + y n = z n$ et qu'ils sont tous non nuls, on peut se ramener à ce qu'ils soient premiers entre eux en divisant par le pgcd des trois, et on a donc: $|x|^n\le max(|x|^n,|y|^n,|z|^n)\le K_\epsilon N_0((xyz)^n)^{1+\epsilon}$ or $N 0 ((x y z) n) = N 0 (x y z)$

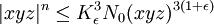
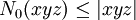
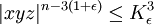
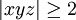
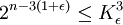
donc, en écrivant la relation précédente pour $| y | n$ et $| z | n$ et en les multipliant toutes les trois, on obtient: $|xyz|^n\le K_\epsilon^3 N_0(xyz)^{3(1+\epsilon)}$ et $N_0(xyz)\le |xyz|$ donc $|xyz|^{n-3(1+\epsilon)}\le K_\epsilon^3$ or x, y et z sont tous non nuls et on vérifie aisément qu'ils ne peuvent être tous de valeur absolue égale à 1, donc $|xyz|\ge 2$ . Finalement, on obtient: $2^{n-3(1+\epsilon)}\le K_\epsilon^3$ , ce qui fournit une valeur limite à n dépendant explicitement de $K ε$ .

Conjecture abc - Définition

Formulation

Analogie avec les polynômes

Une des principales conséquences: le théorème de Fermat

Autres conséquences de la conjecture