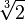Duplication du cube - Définition
La duplication du cube est un problème classique de mathématiques. C'est un problème géométrique, faisant partie des trois grands problèmes de l'Antiquité, avec la quadrature du cercle et la trisection de l'angle. Ce problème consiste à construire un cube, dont le volume est deux fois plus grand qu'un cube donné, à l'aide d'une règle et d'un compas. Cela revient donc à chercher à multiplier l'arête du cube par
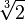
Ce problème se posa pour la première fois lors d'une épidémie de peste à Athènes. Les Athéniens demandèrent à l'oracle de Delphes comment faire cesser cette épidémie. La réponse de l'oracle fut qu'il fallait doubler l'autel consacré à Apollon dans l'île de Délos, autel dont la forme était un cube parfait. Beaucoup de mathématiciens se penchèrent sur la question, Hippias d'Élis, Archytas de Tarente, Ménechme, Eudoxe de Cnide. Mais toutes les solutions apportées utilisaient d'autres méthodes que la règle et le compas, et n'étaient donc pas concrètement réalisables. L'épidémie cessa finalement, mais de nombreux mathématiciens continuèrent à essayer de trouver une solution au problème.
En 1837, Pierre-Laurent Wantzel établit un théorème donnant la forme des équations des problèmes impossibles à résoudre à la règle et au compas. Il démontre que