Identité remarquable (mathématiques élémentaires) - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
On appelle identités remarquables, en mathématiques, les égalités suivantes (et d'autres égalités analogues). Elles s'obtiennent, grâce à la propriété de distributivité de la multiplication, en développant et factorisant des expressions.
Pour a et b deux nombres réels (ou plus généralement deux éléments d'un anneau commutatif quelconque), on a :
- Second degré
- (a + b)2 = a2 + 2ab + b2
- (a − b)2 = a2 − 2ab + b2
- (a − b)(a + b) = a2 − b2
- Troisième degré
- (a + b)3 = a3 + 3a2b + 3ab2 + b3
- (a − b)3 = a3 − 3a2b + 3ab2 − b3
- a3 + b3 = (a + b)(a2 − ab + b2)
- a3 − b3 = (a − b)(a2 + ab + b2)
Utilité
Les identités remarquables sont une sorte de formule magique pour rendre les factorisation plus simples. Bien connaître ses identités remarquables permet d'obtenir un gain de vitesse important ! Face à un problème de factorisation, il peut être utile de noter les identités remarquables sur un brouillon afin de pouvoir les comparer à l'expression à factoriser. Elles permettent aussi de simplifier considérablement des équations.
Démonstrations algébriques
(a + b)2 = (a + b)(a + b) = a2 + ab + ba + b2 = a2 + 2ab + b2 (grâce à la commutativité de la multiplication : ab = ba)
(a − b)2 = (a − b)(a − b) = a2 − ab − ba + b2 = a2 − 2ab + b2
(a − b)(a + b) = a2 + ab − ba − b2 = a2 − b2
(a + b)3 = (a + b)2(a + b) = (a2 + 2ab + b2)(a + b) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3
(a − b)3 = (a − b)2(a − b) = (a2 − 2ab + b2)(a − b) = a3 − 2a2b + ab2 − a2b + 2ab2 − b3 = a3 − 3a2b + 3ab2 − b3
(a + b)(a2 − ab + b2) = a3 − a2b + ab2 + a2b − ab2 + b3 = a3 + b3
L'identité avec (a3 − b3) s'obtient de celle avec (a3 + b3) en remplaçant b par -b.
Démonstrations géométriques
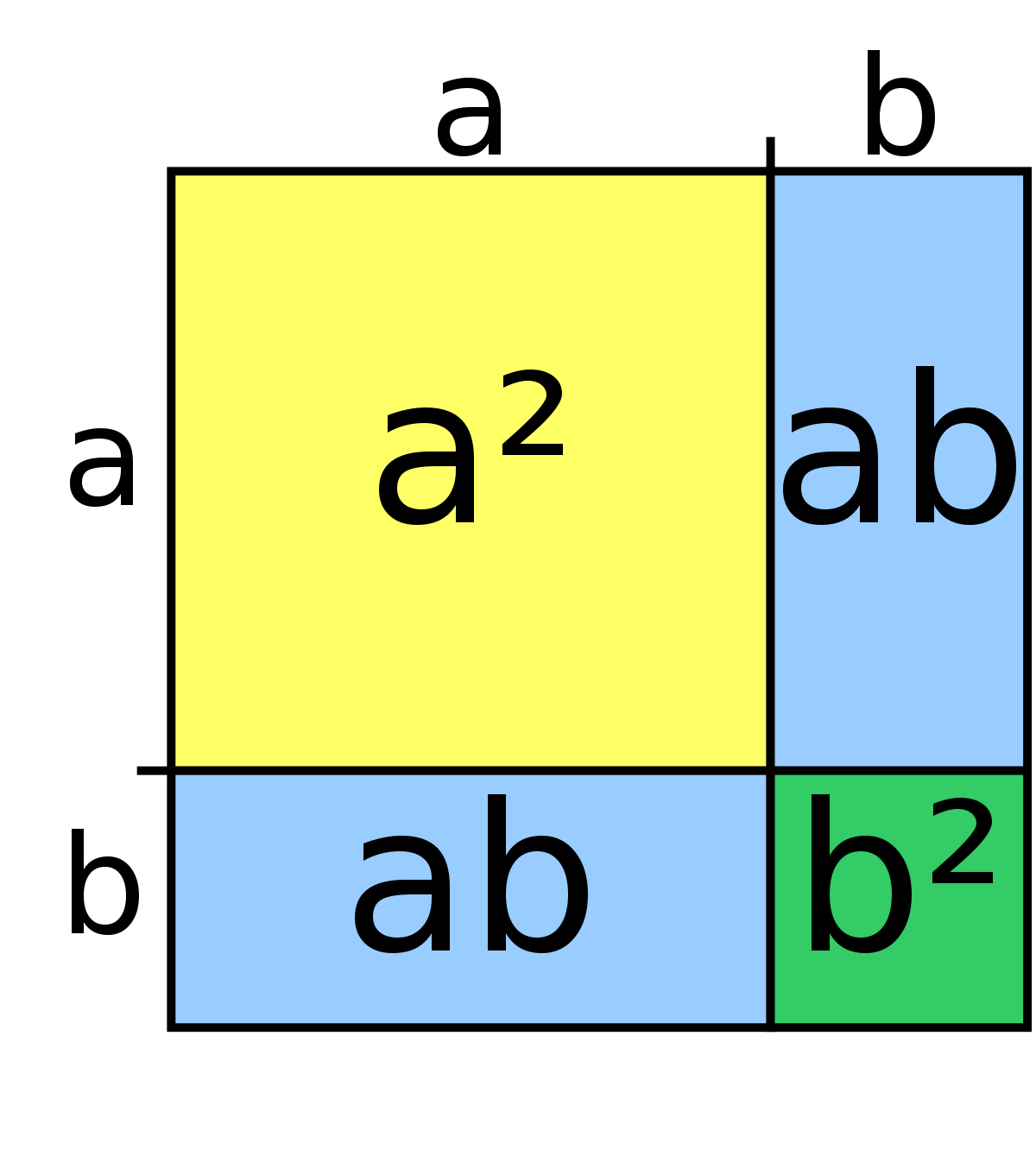
- Carré de somme ou de différence à la manière du livre II des Éléments d'Euclide et aussi (Maths élémentaire d'Euclide). La figure ci-contre permet de justifier les deux premiers éléments du formulaire.
- On peut convenir que la figure représente un carré dont le côté est somme de deux valeurs a et b. Son aire vaut donc (a+b)². Mais elle s'obtient aussi par l'addition de l'aire du carré jaune (a²), des aires des rectangles bleus (ab pour chacun) et de l'aire du carré vert (b²).
- On peut convenir aussi que a désigne le côté du grand carré et b le côté du carré jaune. L'aire du carré vert vaut donc (a-b)². Mais cette valeur peut s'obtenir en retranchant du grand carré d'aire a² deux rectangles jaunes et bleus d'aire ab et en rajoutant une fois b² car l'aire de ce carré jaune a été soustraite deux fois.