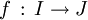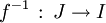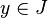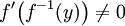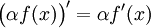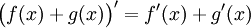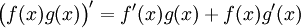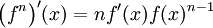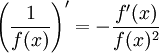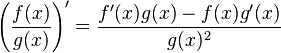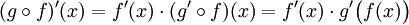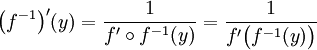Opérations sur les dérivées - Définition

On peut déterminer la dérivée de n'importe quelle fonction en effectuant des opérations sur les dérivées présentées ici.

Dans tout l'article, I et J seront des intervalles réels.

Les démonstrations de ces propriétés dérivent des opérations sur les limites.

Linéarité

Multiplication par un réel

Soient une fonction dérivable sur I et α un réel fixé. Le produit αf est dérivable sur I et :

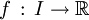
Somme

Soient et deux fonctions dérivables sur I. Leur somme f + g est dérivable sur I et :

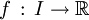
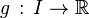
Produit et quotient

Produit

Soient et deux fonctions dérivables sur I. Leur produit fg est dérivable sur I et

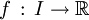
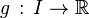
Puissance

Soit une fonction dérivable sur I. La fonction est dérivable sur I, sa dérivée est donnée par

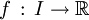
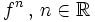
Inverse

Soit une fonction dérivable sur I. L'inverse de f est dérivable sur l'ensemble des tels que et sa dérivée est donnée par

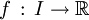
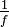
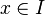
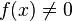
Quotient

Soient et deux fonctions dérivables sur I. Le quotient est dérivable sur l'ensemble des tels que et sa dérivée est donnée par

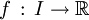
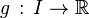
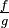
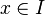
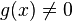
Composition

Composée

Soient et deux fonctions dérivables respectivement sur I et J. On suppose que l'image par f de l'intervalle I est incluse dans J : .

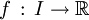
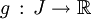
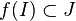
Alors la fonction composée définie par est dérivable sur I et :

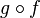
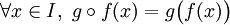
Bijection réciproque

Soit une fonction bijective dérivable sur I. Alors la fonction réciproque est dérivable en tout point tel que et pour un tel y :