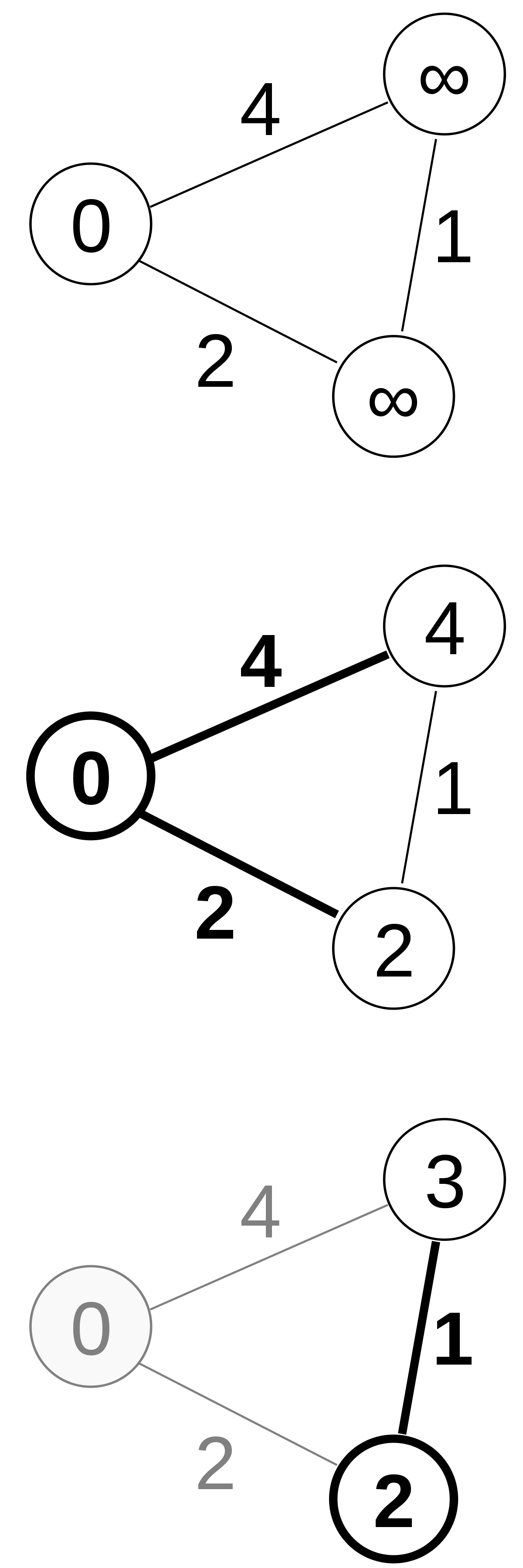
Algorithme de Dijkstra - Définition
L'algorithme de Dijkstra sert à résoudre le problème du plus court chemin entre deux sommets d'un graphe connexe dont le poids lié aux arêtes est positif ou nul.
Pour illustrer l'intérêt de cet algorithme, on peut prendre pour exemple le réseau routier d'une région : chaque sommet est une ville et chaque arc est une route dont le poids est le kilométrage. L'algorithme de Dijkstra permet alors de trouver le plus court chemin d'une ville à une autre.
L'algorithme porte le nom de son inventeur, l'informaticien néerlandais Edsger Dijkstra et a été publié en 1959[1].
Notations
Le graphe est noté G = (S,A) où :
- l'ensemble S est l'ensemble des sommets du graphe G ;
- l'ensemble A est l'ensemble des arêtes de G tel que : si (s1,s2) est dans A, alors il existe une arête depuis le nœud s1 vers le nœud s2 ;
- on définit la fonction Poids(s1,s2) définie sur A qui renvoie le poids positif de l'arête reliant s1 à s2 (et un poids infini pour les paires de sommets qui ne sont pas connectées par une arête).
Principes
Le poids du chemin entre deux sommets est la somme des poids des arêtes qui le composent. Pour une paire donnée de sommets sdeb (le sommet du départ) sfin (sommet d'arrivée) appartenant à S, l'algorithme trouve le chemin depuis sdeb vers sfin de moindre poids (autrement dit le chemin le plus léger ou encore le plus court).
L'algorithme fonctionne en construisant un sous-graphe P de manière à ce que la distance entre un sommet s de P depuis sdeb soit connue et soit un minimum dans G. Initialement P contient simplement le nœud sdeb isolé, et la distance de sdeb à lui-même vaut zéro. Des arcs sont ajoutés à P à chaque étape :
- 1. en identifiant toutes les arêtes ai = (si1,si2) dans
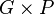
- 2. en choisissant l'arête aj = (sj1,sj2) dans
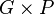
L'algorithme se termine soit quand P devient un arbre couvrant de G, soit quand tous les nœuds d'intérêt[2] sont dans P.
Algorithme
Fonction annexes
L'algorithme utilise les fonctions annexes suivantes.
Initialisation de l'algorithme
Initialisation(G,sdeb) 1 pour chaque point s de G 2 faire d[s]:= infini /* on initialise les sommets autres que sdeb à 0 */[3] 3 prédecesseur[s]:= 0 /* car on ne connaît au départ aucun chemin entre s et sdeb */ 4 d[sdeb]:= 0 /* sdeb étant le point le plus proche de sdeb */
Recherche du nœud le plus proche
- On recherche le nœud le plus proche (relié par l'arête de poids le plus faible) de sdeb parmi les nœuds situés dans un ensemble Q, constitué des nœuds éloigné d'une arête des éléments de P. On utilise pour cela la fonction Trouve_min(). Le nœud trouvé est alors effacé de l'ensemble Q et est alors retourné à la fonction principale comme résultat de la fonction.
Mise à jour des distances
- On met à jour des distances entre sdeb et s2 en se posant la question : vaut-il mieux passer par s1 ou pas ?
maj_distances(s1,s2) 1 si d[s2] > d[s1] + Poids(s1,s2) 2 alors d[s2]:= d[s1] + Poids(s1,s2) 3 prédecesseur[s2]:= s1 /* on fait passer le chemin par s1 */
Fonction principale
Voici la fonction principale utilisant les précédentes fonctions annexes :
Dijkstra(G,Poids,sdeb) 1 Initialisation(G,sdeb) 2 P:= ensemble vide 3 Q:= ensemble de tous les nœuds 4 tant que Q n'est pas un ensemble vide 5 faire s1:= Trouve_min(Q) 6 P:= P union {s1} 7 pour chaque nœud s2 voisin de s1 8 faire maj_distances(s1,s2)
Le plus court chemin de sdeb à sfin peut ensuite se calculer itérativement selon l'algorithme suivant, avec A la suite représentant le plus court chemin de sdeb à sfin:
1 A = suite vide 2 s:= sfin 3 A = s + A /* insère s au début de A */ 4 tant que s != sdeb 5 s = prédecesseur[s] /* on continue de suivre le chemin */ 6 A = s + A
Améliorations de l'algorithme
Il est possible d'améliorer légèrement l'algorithme principal en arrêtant la recherche lorsque l'égalité s1 = sfin est vérifiée, à condition bien sûr de ne chercher que la distance minimale entre sdeb et sfin.
L'algorithme de Dijkstra pourra être mis en œuvre efficacement en stockant le graphe sous forme de listes d'adjacence et en utilisant un tas comme une file à priorités pour réaliser la fonction Trouve_min. Si le graphe possède m arcs et n nœuds, en supposant que les comparaisons des poids d'arcs soient à temps constant, alors la complexité de l'algorithme est :
![\sigma [(m+n)\times ln(n)]](https://static.techno-science.net/illustration/Definitions/autres/5/5d5a9c4709f0b806f034406f9d74d766_6515f96be068448b3e07f824f2ced86d.png)
![\sigma [m+n\times ln(n)]](https://static.techno-science.net/illustration/Definitions/autres/2/2e2ab33529f21ee9cb4c9b6832e538af_c65e7a4475e40c3b9c4182313de12580.png)
Exemple
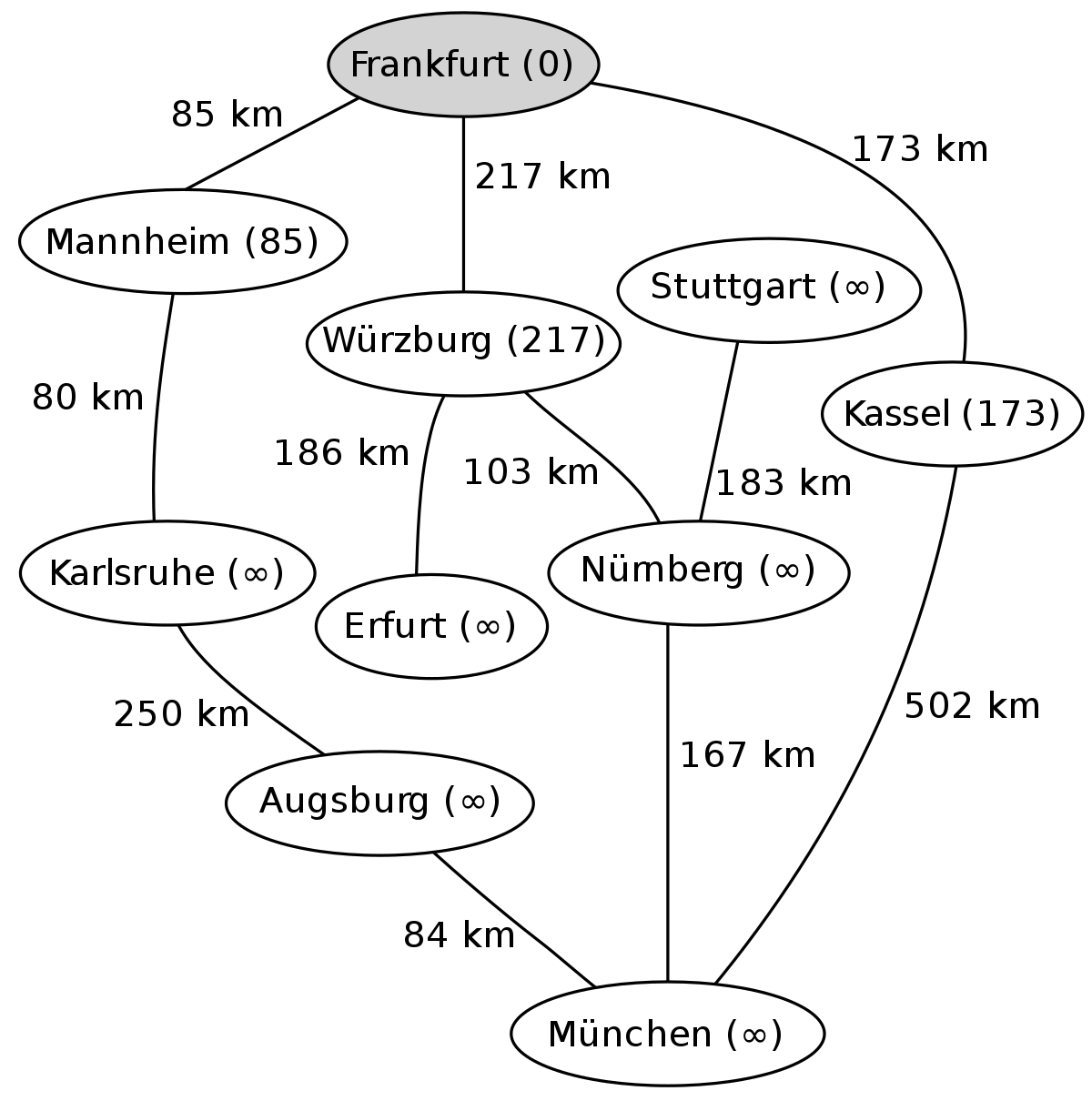
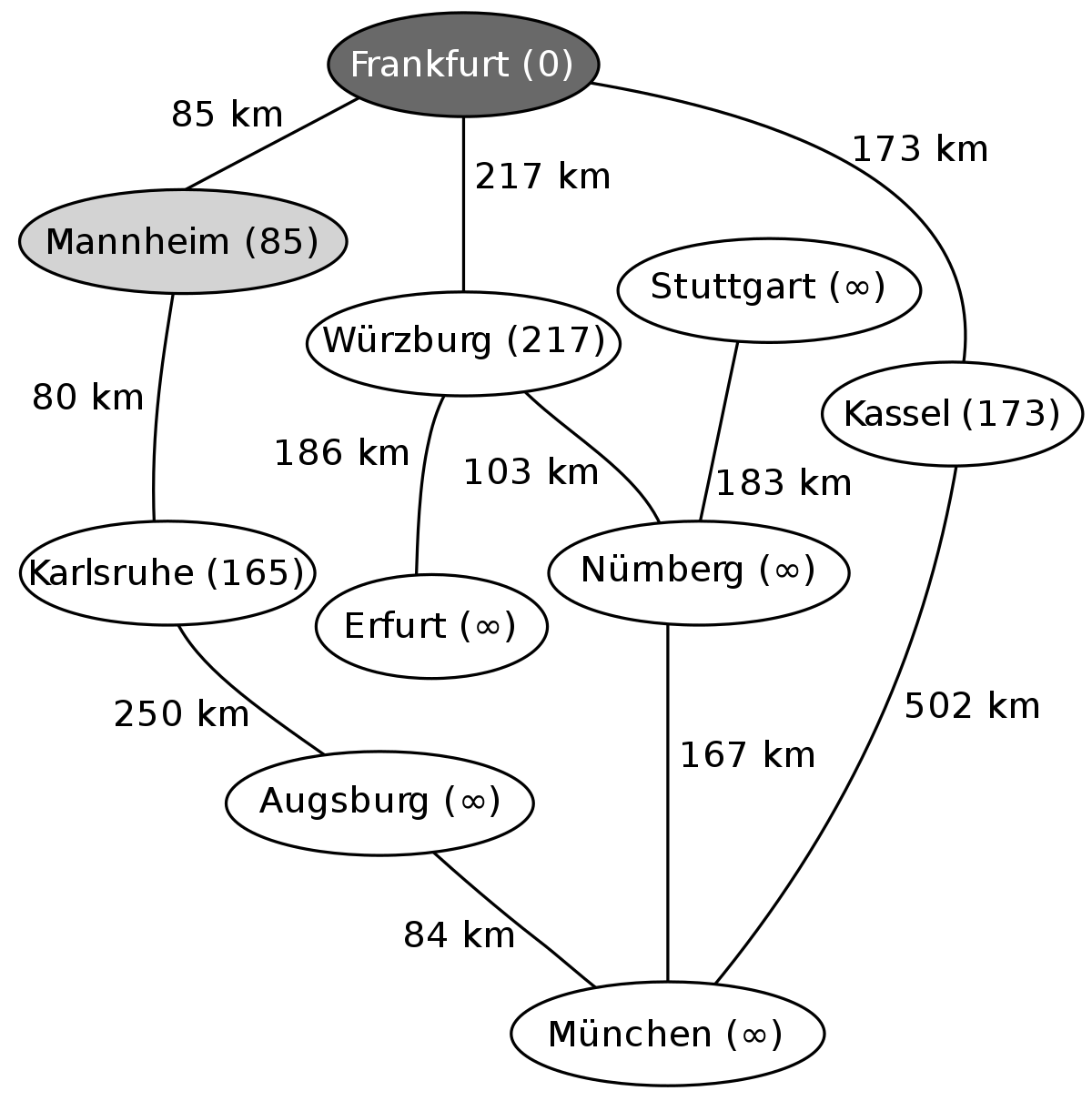
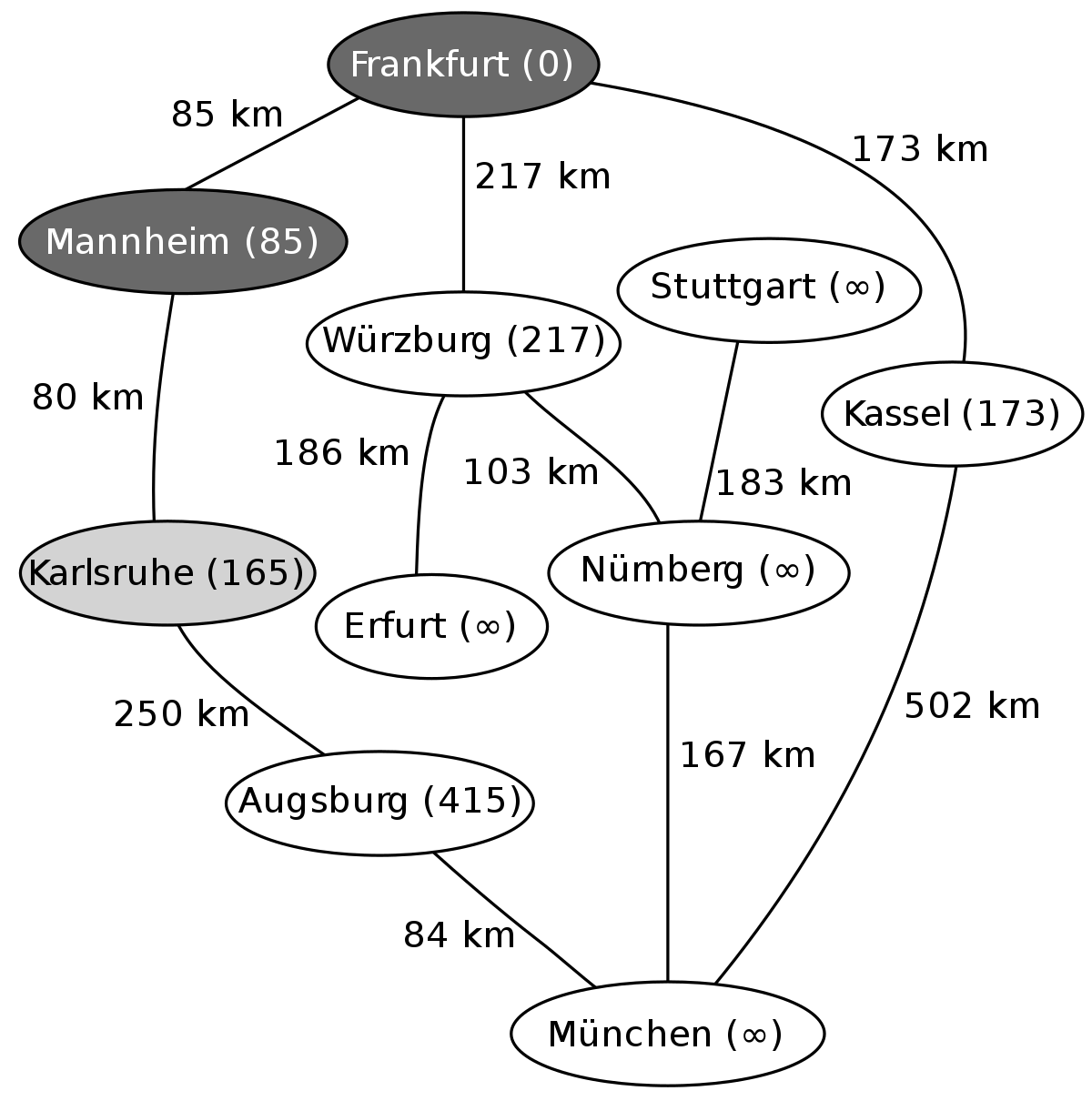
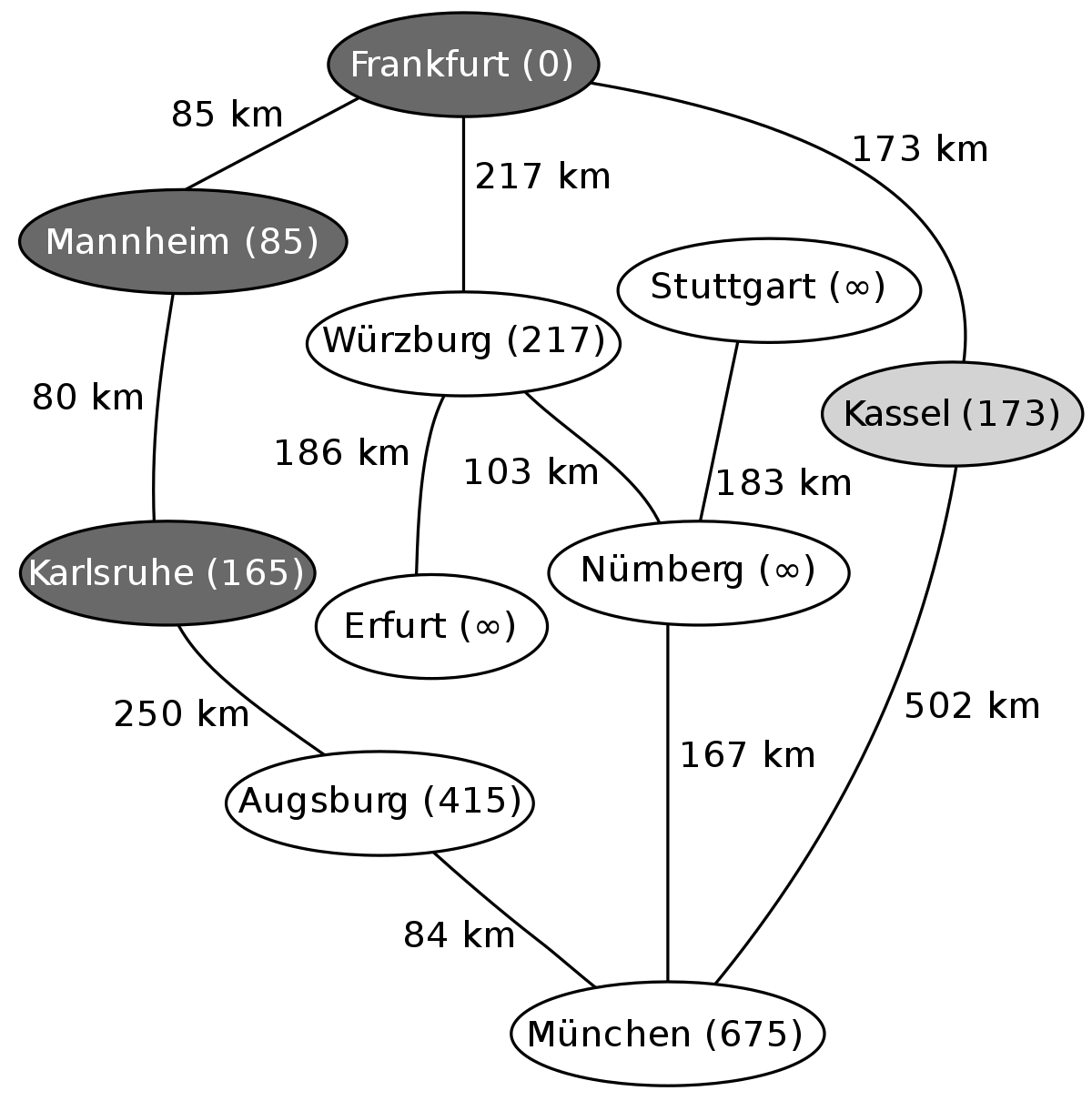
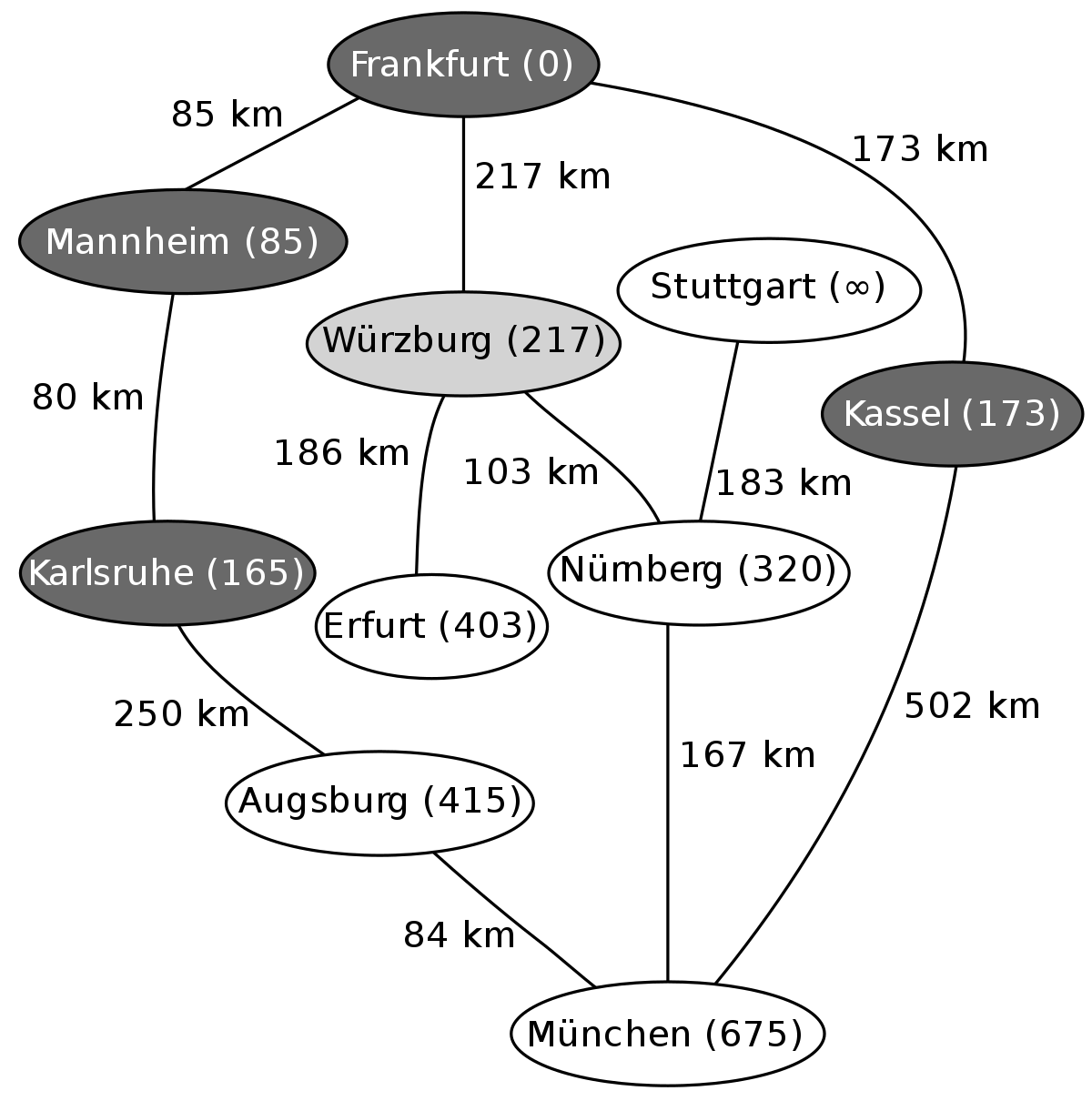
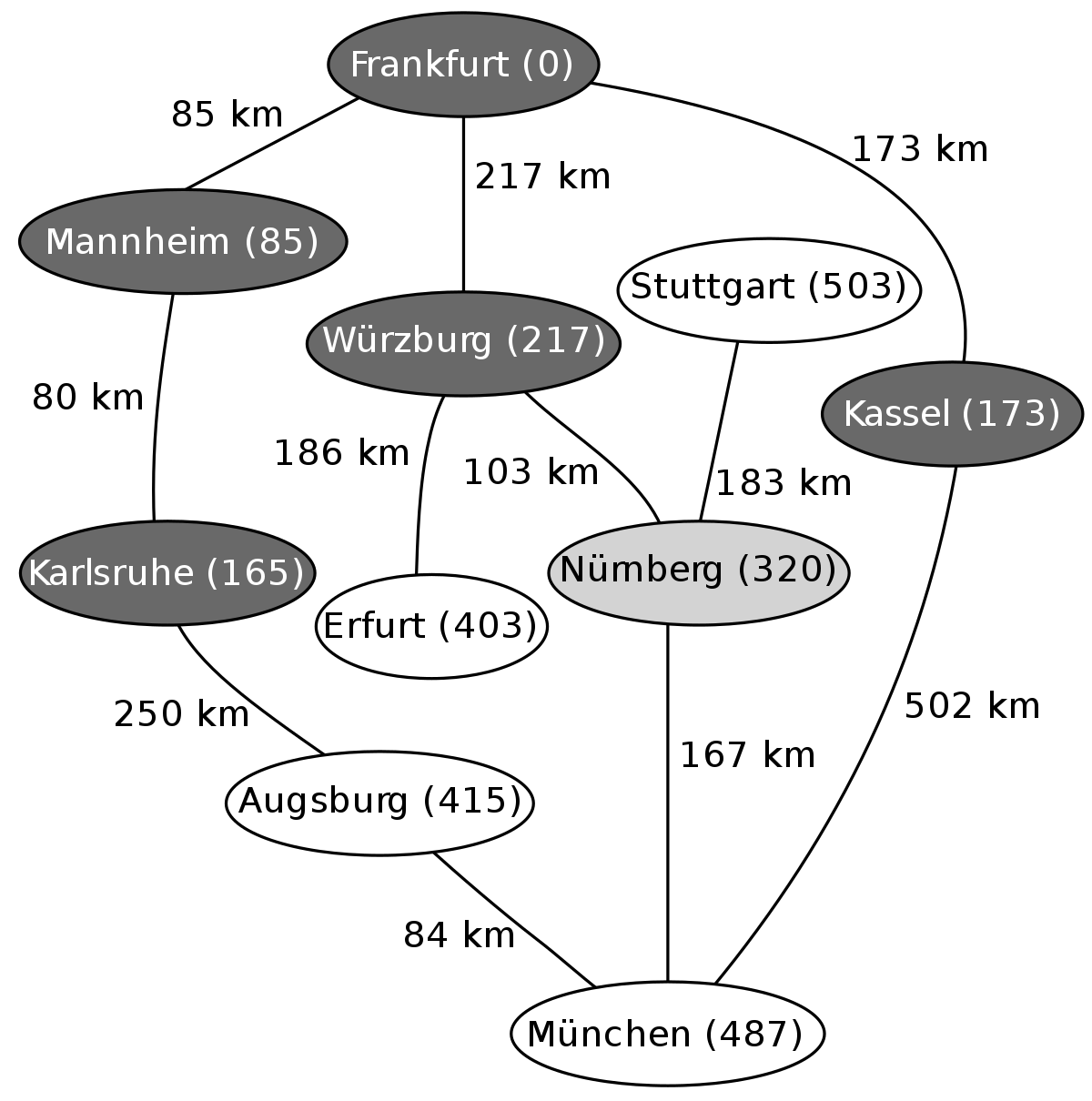
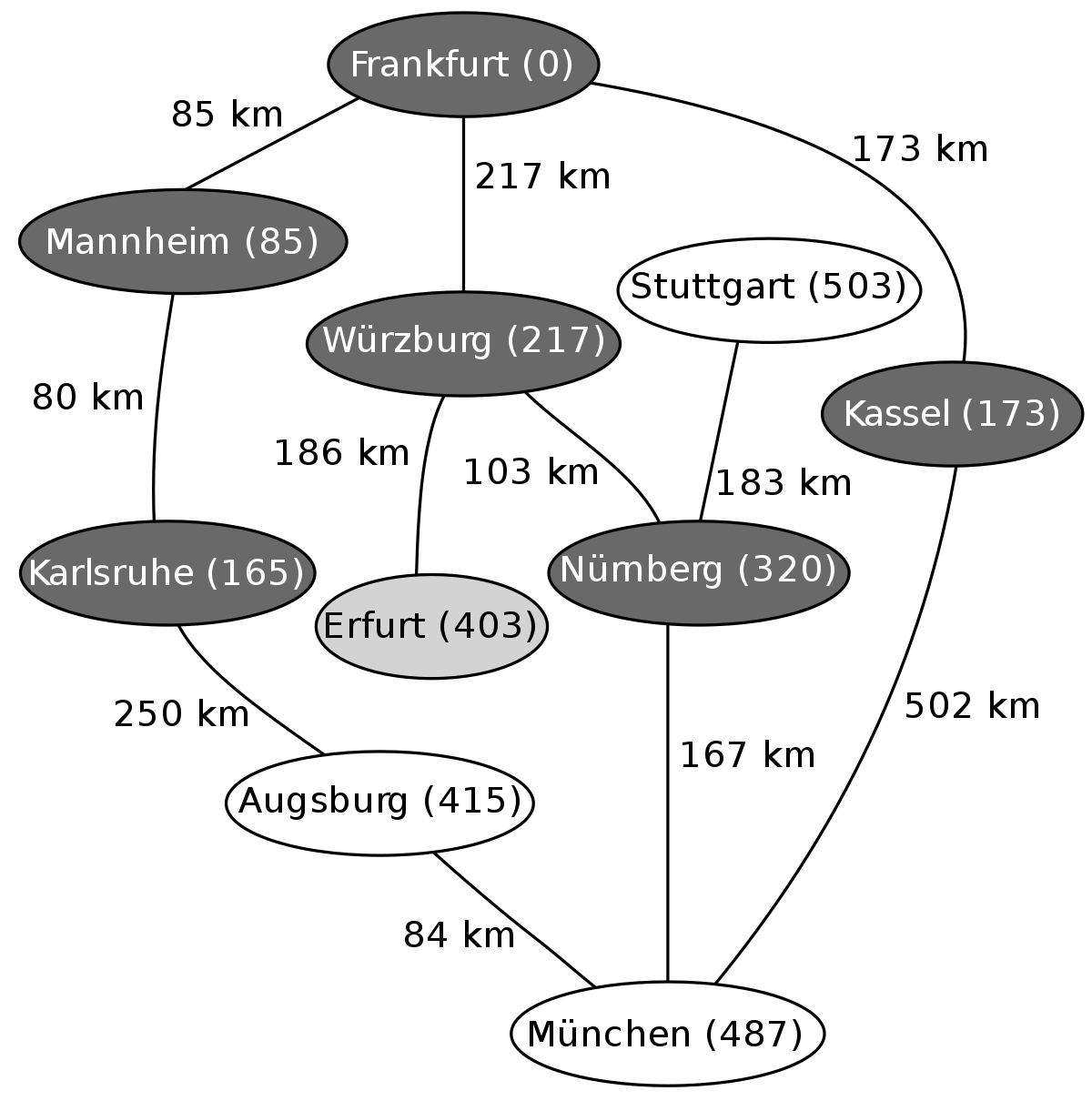
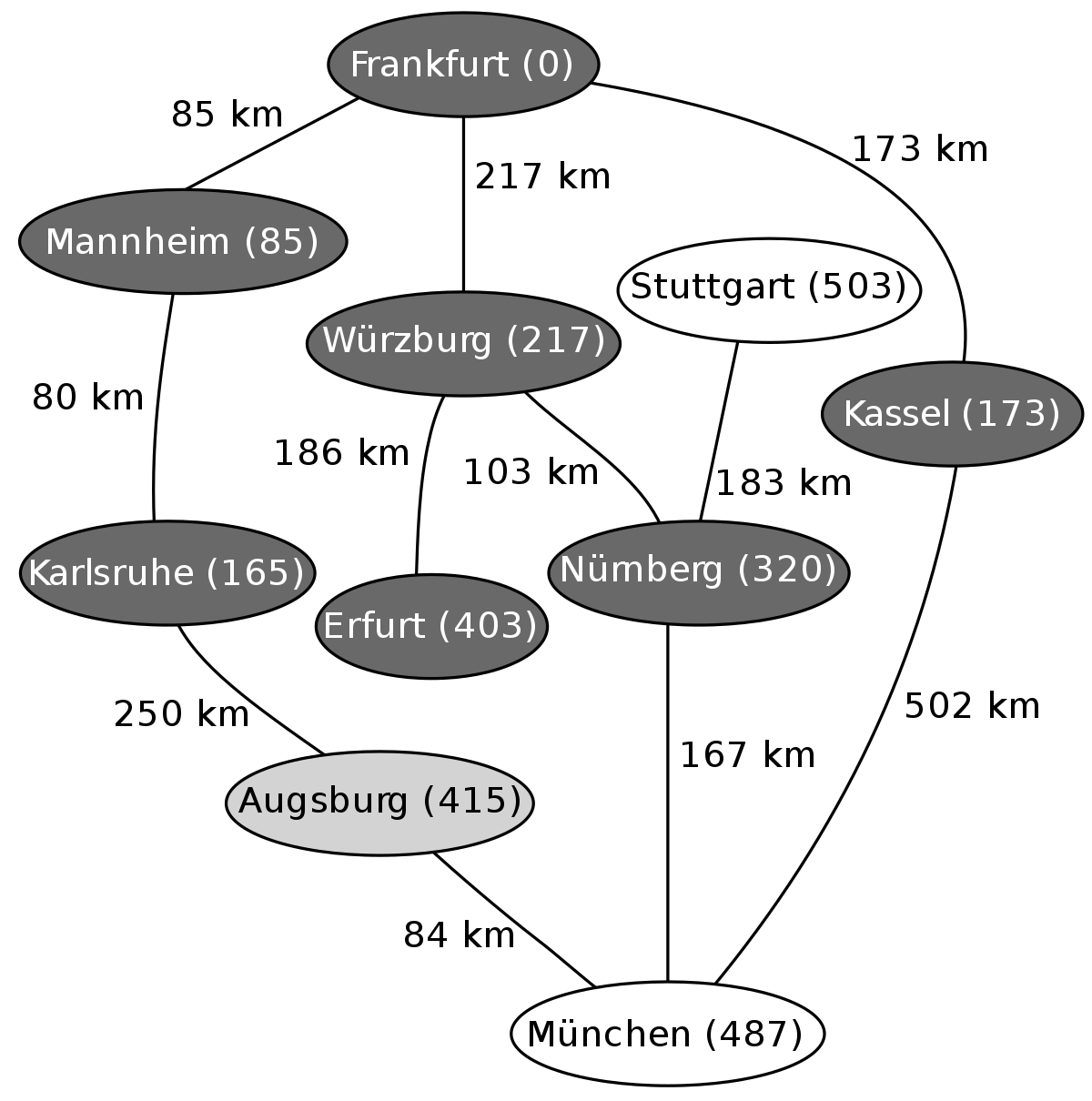
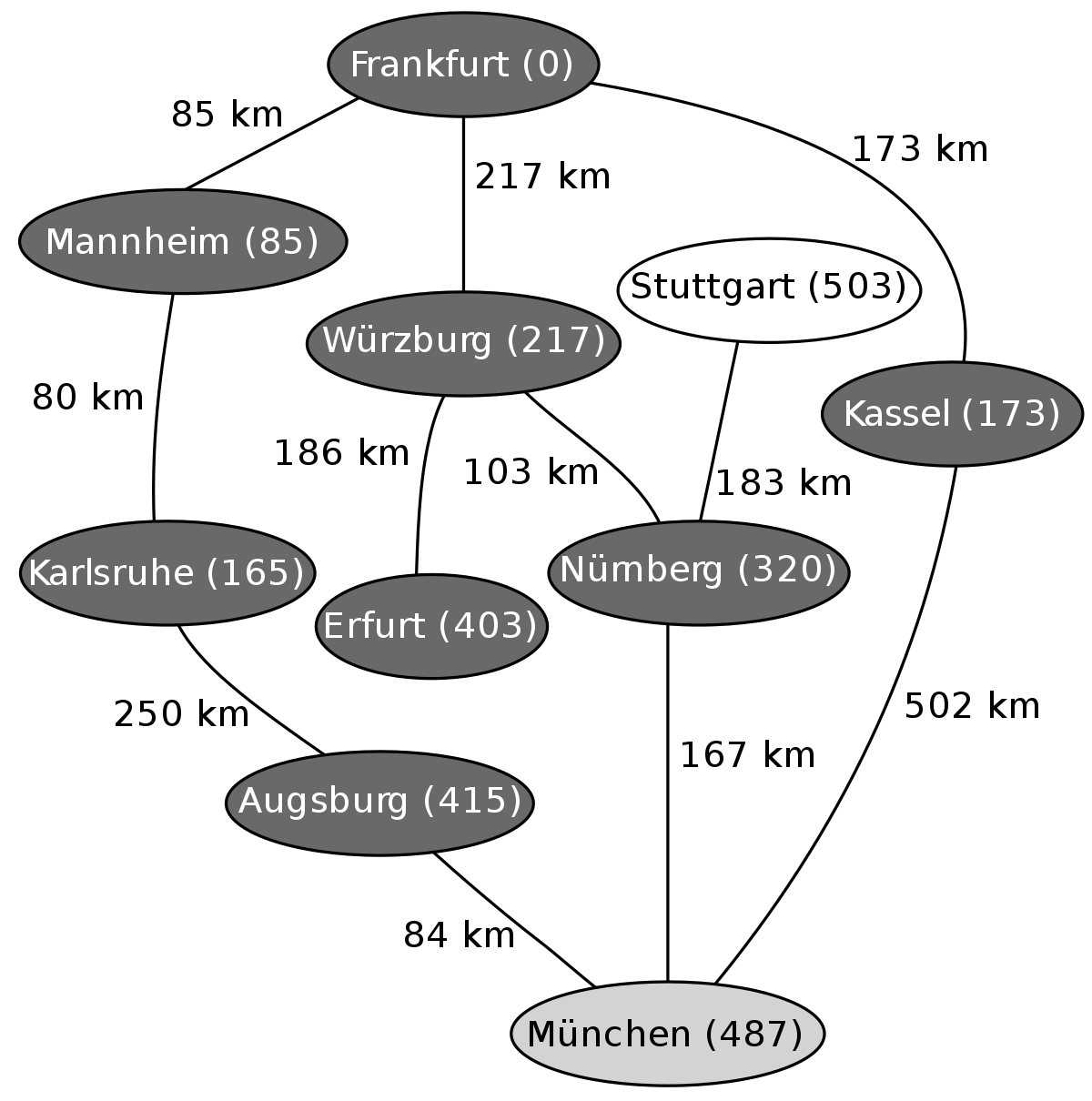
L'exemple suivant montre les étapes successives dans la résolution du chemin le plus court dans un graphe. Les nœuds symbolisent des villes en Allemagne et les arêtes indiquent la distance entre les villes. On veut aller de Francfort (Frankfurt) à Munich (München).
Codes
Pseudo-code
fonction Dijkstra (nœuds, fils, distance, debut, fin)
Pour n parcourant nœuds
n.parcouru = infini // Peut être implémenté avec -1
n.precedent = 0
Fin pour
debut.parcouru = 0
DejaVu = liste vide
PasEncoreVu = nœuds
Tant que PasEncoreVu != liste vide
n1 = minimum(PasEncoreVu) // Le nœud dans PasEncoreVu avec parcouru le plus petit
DejaVu.ajouter(n1)
PasEncoreVu.enlever(n1)
Pour n2 parcourant fils(n1) // Les nœuds reliés à n1 par un arc
Si n2.parcouru > n1.parcouru + distance(n1, n2) // distance correspond au poids de l'arc reliant n1 et n2
n2.parcouru = n1.parcouru + distance(n1, n2)
n2.precedent = n1 // Dis que pour aller à n2, il faut passer par n1
Fin si
Fin pour
Fin tant que
chemin = liste vide
n = fin
Tant que n != debut
chemin.ajouterAvant(n)
n = n.precedent
Fin tant que
Retourner chemin
Fin fonction Dijkstra
Implémentation Caml
Voici le code d'implémentation Caml :
(* on suppose données des files de priorité *)
module H: sig
type 'a t
val empty: 'a t
val is_empty: 'a t -> bool
val add: int * 'a -> 'a t -> 'a t
val extract_min: 'a t -> (int * 'a) * 'a t
end
(* l'adjacence est donnée sous la forme d'une fonction: adj v est la liste des voisins de v,
avec leur distance ; la fonction suivante cherche le plus court chemin de v1 à v2 *)
let dijkstra (adj: 'a -> ('a * int) list) (v1:'a) (v2:'a) =
let visited = Hashtbl.create 97 in
let rec loop h =
if H.is_empty h then raise Not_found;
let (w,(v,p)),h = H.extract_min h in
if v = v2 then
List.rev p, w
else
let h =
if not (Hashtbl.mem visited v) then begin
Hashtbl.add visited v ();
List.fold_left (fun h (e,d) -> H.add (w+d, (e, e::p)) h) h (adj v)
end else
h
in
loop h
in
loop (H.add (0,(v1,(lien))) H.empty)
Applications
Une application des plus courantes de l'algorithme de Dijkstra est le protocole open shortest path first qui permet un routage internet très efficace des informations en cherchant le parcours le plus efficace.
Les routeurs IS-IS utilisent également l'algorithme. Les sites d'itinéraires routiers l'utilise de la même manière et permettent de nombreuses adaptations en ajustant le poids des arcs comme par exemple : trajet le plus économique, le plus rapide...
Apparition dans la culture populaire
L'algorithme de Dijkstra est utilisé par les enquêteurs de la série NUMB3RS, dans l'épiode 23 de la saison 3.