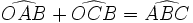Théorème de Thalès (cercle) - Définition
On attribue à Thalès, la démonstration de nombreuses propriétés géométriques.
En France, le théorème de Thalès concerne des propriétés de proportionnalité dans des triangles coupés par des droites parallèles. Mais Thalès s'est aussi intéressé au cercle circonscrit. On appelle aussi théorème de Thalès la propriété suivante:
Un triangle inscrit dans un cercle et dont un côté est un diamètre est un triangle rectangle.
Le demi-cercle dont le diamètre est l'hypoténuse d'un triangle rectangle est parfois appelé "Cercle de Thalès". La demi-sphère dont le diamètre est l'hypoténuse d'un triangle rectangle est parfois appelée "Sphère de Thalès".
Démonstration
Dans la figure, les triangles (OAB) et (OBC) sont isocèles de sommet O, donc nous pouvons écrire les égalités suivantes :
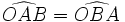
(rem: cette propriété est aussi une propriété démontrée par Thalès)
En sommant ces deux égalités, il vient :
Comme la somme des angles d'un triangle vaut 180°, il vient
- °
puis en divisant par 2 la dernière égalité, on obtient
-
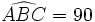
Le triangle est donc bien rectangle en B.
Réciproque
Il existe aussi une réciproque à cette version du théorème de Thalès :
Si ABC est un triangle rectangle en B alors le triangle s'inscrit dans un cercle de diamètre [AC]
Démonstration: on trace la droite passant par le milieu O de [AC] et le milieu A' de [BC]. Comme droite des milieux, elle est parallèle à (AB). Comme (AB) et (BC) sont perpendiculaires, il en est de même de (A'O) et (BC). (A'O) est donc une droite passant par le milieu de [BC] et perpendiculaire à [BC], c'est donc la médiatrice de [BC]. Il suffit de faire le même raisonnement pour la droite passant par O et par C' milieu de [AB] pour prouver que cette droite est la médiatrice de [AB]. Ces deux médiatrices se coupent en O qui est donc le centre du cercle circonscrit au triangle. Comme O est le milieu de [AC], le cercle a bien pour diamètre [AC]