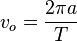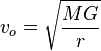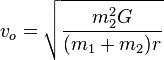Vitesse orbitale - Définition
La vitesse orbitale d'un corps céleste, le plus souvent une planète, un satellite naturel, un satellite artificiel ou une étoile binaire, est la vitesse à laquelle il orbite autour du barycentre d'un système à deux corps, soit donc le plus souvent autour d'un corps plus massif. L'expression peut être employée pour désigner la vitesse orbitale moyenne du corps le long de son orbite ou la vitesse orbitale instantanée, en un point précis de cette orbite.
La vitesse orbitale instantanée peut être determinée par la seconde loi de Kepler, à savoir qu'en une durée déterminée, le segment de droite reliant le barycentre au corps décrit une surface constante, quelle que soit la portion de l'orbite que le corps parcourt pendant cette durée. En conséquence, le corps va plus vite près de son périastre que de son apoastre.
La vitesse orbitale moyenne est déterminée soit en connaissant sa période orbitale et le demi-grand axe de son orbite, soit à partir des masses des deux corps et du demi-grand axe :
où vo est la vitesse orbitale moyenne, a est la longueur du demi-grand axe, T la période orbitale, M la masse du corps autour duquel orbite celui dont on veut calculer la vitesse et G la constante gravitationnelle. Il faut noter cependant que ceci n'est qu'une approximation qui est vérifiée quand la masse du corps orbitant est considérablement plus faible que celle du corps central.
Dans le cas où la masse du corps orbitant n'est pas négligeable devant celle de l'autre corps,
où m1 est ici la masse du corps considéré, m2 celle de l'autre corps et r le rayon entre les deux corps. Il s'agit néanmoins là du cas particulier où les orbites des deux corps sont circulaires et non elliptiques.
|
|