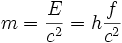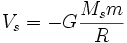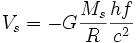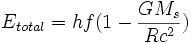Décalage d'Einstein - Définition
Le décalage d'Einstein est un effet prédit par les équations d'Albert Einstein. D'après cette théorie, un photon émis depuis un astre massif arrive décalé vers le rouge à cause des champs gravitationnels.
Dualité du photon
Le photon est à la fois une onde et une particule. En tant qu'onde, la masse d'un photon est nulle ; mais en tant que particule, on a la relation :
- E = hf = mc2
Avec :
- E l'énergie du photon en J ;
- h la constante de Planck ;
- f la fréquence de la lumière en Hz ;
- m la masse du photon en kg ;
- c la célérité du photon dans le vide, en m.s-1.
Ce qui donne :
Energie potentielle de gravitation
Elle est donnée par les équations de Newton :
Avec :
- G la constante de gravitation ;
- Ms la masse d'un astre ;
- m la masse du photon ;
- R la distance entre le centre de gravité de l'astre et du photon.
Le signe - indique que la force gravitationnelle est attractive uniquement. En reprenant l'équation de masse du photon :
L'énergie totale du photon, somme de l'énergie cinétique et de l'énergie potentielle notée Etotal vaut, à la surface d'un astre massif:
L'énergie du photon est toujours constante. Si on considère maintenant que le photon est au voisinage de la Terre, et subit donc une pesanteur bien inférieure, on a :
- Eterre = Eetoile
-
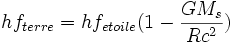
-
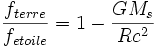
-
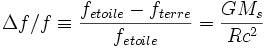
Le photon possède moins d'énergie au voisinage de la Terre, perte qui se caractérise par une baisse de la fréquence, appelée décalage vers le rouge gravitationnel, ou plus souvent décalage d'Einstein.