3-sphère - Définition

Propriétés

Propriétés élémentaires

Le volume tridimensionnel (encore appelé hyperaire) de la 3-sphère de rayon r est : alors que l'hypervolume (le volume de la région 4-dimensionnelle borné par la 3-sphère) est : Chaque intersection non vide d'une 3-sphère avec un hyperplan (tridimensionnel) est une 2-sphère, sauf si l'hyperplan est tangent à la 3-sphère, auquel cas l'intersection est réduite à un point. En déplaçant une 3-sphère à travers un hyperplan fixé, l'intersection est d'abord un point, puis devient une 2-sphère de rayon croissant jusqu'à atteindre le rayon de la 3-sphère lorsque l'hyperplan passe par son centre, et décroit à nouveau pour se réduire à un point quand la 3-sphère quitte l'hyperplan.

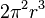
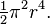
Propriétés topologiques

La 3-sphère est une variété de dimension 3, compacte, connexe, sans bord. Cette variété est également simplement connexe, ce qui (de façon informelle) signifie que tout chemin fermé (ou boucle) sur la 3-sphère peut être continument contracté en un point sans quitter la 3-sphère. La conjecture de Poincaré, démontrée en 2003 par Grigori Perelman, affirme que la 3-sphère est la seule variété (topologique) à trois dimensions possédant ces propriétés (à homéomorphisme près).

La 3-sphère est homéomorphe au compactifié d'Alexandroff de . Plus généralement, on dit qu'un espace topologique homéomorphe à la 3-sphère est une 3-sphère topologique. Les groupes d'homologie de la 3-sphère sont les suivants : H₀(S³,Z) et H₃(S³,Z) sont isomorphes à Z, tandis que H_i(S³,Z) = {0} pour tous les autres indices i. Tout espace topologique ayant ces groupes d'homologie est appelé une 3-sphère homologique. Initialement, Poincaré avait conjecturé que toutes les 3-sphères homologiques étaient homéomorphes à S³, mais il réussit ensuite lui-même à construire un contre-exemple, à présent connu sous le nom de sphère homologique de Poincaré (ce qui montre que la conjecture de Poincaré ne peut être formulée en termes d'homologie seule). On sait désormais qu'il existe une infinité de sphères homologiques. Par exemple, un comblement de Dehn de pente 1/n de n'importe quel nœud de la 3-sphère est une sphère homologique, non homéomorphe à la 3-sphère en général. En ce qui concerne les groupes d'homotopie, on a π₁(S³) = π₂(S³) = {0} et π₃(S³) isomorphe à Z. Les groupes d'indice supérieur (k ≥ 4) sont tous abéliens et finis, mais ne semblent pas suivre de schéma régulier. Pour une discussion plus approfondie, voir groupes d'homotopie des sphères.

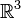
Propriétés géométriques

La 3-sphère est dotée naturellement d'une structure de variété différentielle ; c'est d'ailleurs en fait une sous-variété compacte de R⁴. La métrique euclidienne de R⁴ induit sur la 3-sphère une métrique lui donnant une structure de variété riemannienne. Comme pour toutes les sphères, la 3-sphère a une courbure constante positive c égale à 1/r², où r est le rayon. La plupart des propriétés géométriques intéressantes de la 3-sphère viennent de ce qu'elle possède une structure naturelle de groupe de Lie, qui lui est donnée par la multiplication des quaternions (voir la section suivante sur la ). Contrairement à la 2-sphère, on peut construire sur la 3-sphère des champs de vecteurs ne s'annulant nulle part (il s'agit plus précisément de sections du fibré tangent). On peut même construire trois tels champs qui soient linéairement indépendants, formant ainsi une base pour l'algèbre de Lie de la 3-sphère. Cela implique que la 3-sphère est parallélisable. Il en résulte également que le fibré tangent de la 3-sphère est trivial.

Il existe une action intéressante du groupe du cercle, T, sur S³, donnant à la 3-sphère une structure de fibré en cercles, connue sous le nom de fibration de Hopf. En considérant S³ comme un sous-ensemble de C², l'action est donnée par :

.

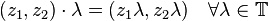
L'espace des orbites de cette action est homéomorphe à la 2-sphère S². Comme S³ n'est pas homéomorphe à S²×S¹, la fibration de Hopf est non-triviale.