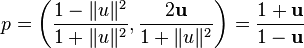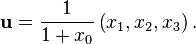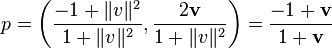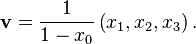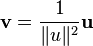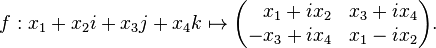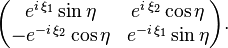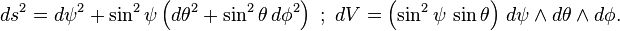3-sphère - Définition

Structure de groupe

L'ensemble des quaternions unitaires forment un groupe (non-abélien) pour la multiplication, et la 3-sphère hérite donc de cette structure (de manière évidemment non canonique). De plus, cette multiplication étant différentiable (et même analytique), S³ peut être considérée comme un groupe de Lie réel ; c'est un groupe de Lie non abélien, compact, de dimension 3. Ce groupe, appelé parfois groupe symplectique ou groupe hyperunitaire, est généralement noté Sp(1) ou U(1, H). Les seules hypersphères admettant une structure de groupe de Lie sont d'ailleurs le cercle S¹ (considéré comme l'ensemble des nombres complexes de module 1, et S³, l'ensemble des quaternions unitaires. On pourrait penser que S⁷, l'ensemble des octonions unitaires, formerait également un groupe de Lie, mais cela échoue, car la multiplication des octonions n'est pas associative ; en revanche, cette multiplication donne à S⁷ l'importante propriété d'être parallélisable ; les seules sphères qui le soient sont S¹, S³, et S⁷.

En utilisant une représentation matricielle des quaternions, H, on obtient une représentation matricielle de S³. Un choix pratique est donné par les matrices de Pauli :

Cette application est un morphisme d'algèbre injectif de H vers l'ensemble des matrices complexes 2×2. La valeur absolue d'un quaternion q est égale à la racine carrée du déterminant de la matrice f(q) (l'image de q par f), et donc l'ensemble des quaternions unitaires correspond aux matrices de cette forme de déterminant 1 ; ce sous-groupe de matrice est précisément le groupe spécial unitaire SU(2). Ainsi, S³ est isomorphe à SU(2) en tant que groupe de Lie. Utilisant les coordonnées hypersphériques (η, ξ₁, ξ₂), nous pouvons alors écrire tout élément de SU(2) sous la forme

Une autre façon d'énoncer ce résultat est d'exprimer la représentation matricielle d'un élément de SU(2) comme combinaison linéaire de matrices de Pauli : on voit qu'un élément arbitraire peut s'écrire comme  ; la condition que le déterminant de U soit +1 implique que les coefficients α_i soient contraints d'appartenir à une 3-sphère.

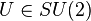
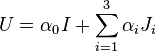
Systèmes de coordonnées sur la 3-sphère

Les quatre coordonnées euclidiennes des points de S³ (considérée comme plongée dans R⁴) sont redondantes, puisque soumises à la condition . En tant que variété de dimension 3, il devrait être possible de paramétrer S³ par 3 coordonnées, tout comme on peut paramétrer la sphère usuelle à l'aide de deux coordonnées telles que la latitude et la longitude. La 3-sphère n'étant pas homéomorphe à l'espace, il est cependant impossible de trouver un unique système de coordonnées (continues) la couvrant en entier, et, comme pour la 2-sphère, il est nécessaire d'utiliser au moins deux cartes locales. Certains choix commodes sont détaillés ci-dessous.

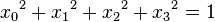
Coordonnées hypersphériques

Par analogie avec les coordonnées sphériques, il est possible de repérer les points de la 3-sphère par trois angles ψ, θ et φ (ce choix n'est nullement unique) définis par

,

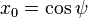
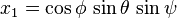
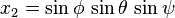
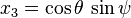
où ψ et θ sont compris dans l'intervalle [0,π], tandis que φ parcourt [0,2π]. On remarquera que pour ψ fixé, θ et φ sont des coordonnées sphériques sur une 2-sphère de rayon sin(ψ), en dehors des cas dégénérés où ψ vaut 0 ou π, correspondant à un seul point.

Le tenseur métrique et la forme volume sur la 3-sphère correspondant à ces coordonnées sont respectivement donnés par :

Ces coordonnées peuvent aussi être élégamment décrites en termes de quaternions : tout quaternion unité peut être écrit comme un verseur : q = e^τψ = cos ψ + τ sin ψ, où τ est un quaternion imaginaire (de partie réelle nulle) et unitaire (c'est-à-dire un quaternion vérifiant τ² = −1) ; ceci est l'analogue pour les quaternions de la formule d'Euler.
L'ensemble des quaternions unitaires imaginaires formant la 2-sphère unité de Im H, on peut écrire tous les t précédents  : τ = cos φ sin θ i + sin φ sin θ j + cos θ k. Sous cette forme, le quaternion unitaire q est donné par :q = e^τψ = x₀ + x₁ i + x₂ j + x₃ k, où les x_i correspondent aux formules données plus haut. Quand on utilise q pour décrire des rotations dans l'espace (voir quaternions et rotation dans l'espace), il correspond alors à une rotation d'angle 2ψ autour de t.

Comme pour la sphère ordinaire, l'ensemble des points où une seule des coordonnées hypersphériques varie est un cercle ; on parle respectivement de cercle parallèle, de cercle méridien et de cercle hyperméridien si la coordonnée variable est φ, θ ou ψ.

Coordonnées de Hopf

Un autre choix de coordonnées hypersphériques, (η, ξ₁, ξ₂), utilise le plongement de S³ dans C². En coordonnées complexes (z₁, z₂) ∈ C² , nous écrivons : et Ici, η appartient à l'intervalle [0,π / 2], et ξ₁ et ξ₂ sont deux angles quelconques de [0,2π]. Ces coordonnées sont utiles pour décrire la 3-sphère en tant que fibration de Hopf : Pour toute valeur de η autre que 0 ou π / 2, les coordonnées (ξ₁, ξ₂) forment une description paramétrique d'un tore (à 2 dimensions); tandis que les cas dégénérés correspondent à des cercles. Dans ce système de coordonnées, le tenseur métrique et la forme volume sont respectivement

.

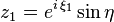
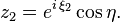
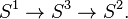
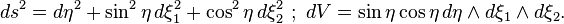
Coordonnées stéréographiques

La projection stéréographique de S³ à partir d'un pôle sur l'hyperplan équatorial correspondant donne un autre ensemble commode de coordonnées. Ainsi, si nous projetons à partir du point (−1, 0, 0, 0), nous pouvons écrire un point p de S³ comme : , où u = (u₁, u₂, u₃) est un vecteur de R³ et ||u||² = u₁² + u₂² + u₃². Dans la seconde égalité, nous avons identifié p avec un quaternion unitaire et u = u₁ i + u₂ j + u₃ k avec un quaternion sans partie réelle (il faut remarquer que cette écriture est justifiée car le numérateur et le dénominateur commutent ici, même si la multiplication des quaternions est non-commutative en général). La bijection réciproque envoie p = (x₀, x₁, x₂, x₃) dans S³ sur : Nous pourrions également avoir pris comme centre de projection le point (1, 0, 0, 0), auquel cas p serait donné par : , où v = (v₁, v₂, v₃) est un autre vecteur de R³ ; la bijection réciproque envoie ici p sur : Il faut remarquer que les coordonnées u sont définies partout sauf en (−1, 0, 0, 0) et que les coordonnées v le sont partout sauf en (1, 0, 0, 0). Ceci définit donc un atlas sur S³ formé de deux cartes locales, qui recouvrent S³ tout entier ; la fonction de transition entre les deux cartes est donnée par : et vice-versa.