Adhérence, intérieur et frontière d'un convexe - Définition
La liste des auteurs de cet article est disponible ici.
Adhérence d'un convexe
Proposition — Dans un espace vectoriel topologique, l'adhérence d'un convexe est convexe.
Notons C le convexe, et soit x et y deux points de
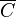
Soit maintenant z un point du segment [x,y] qui peut donc être écrit sous la forme z = λx + (1 − λ)y pour un certain λ de [0,1].
Version simplifiée de la démonstration, valable pour les seuls espaces métrisables (et en particulier en dimension finie)
On peut écrire
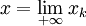
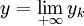
Alors
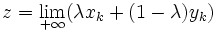
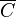
Version valable dans tout espace vectoriel topologique
Dans l'intention de montrer que z appartient à
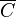
L'application :
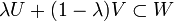
Enchaînement d'opérations successives
Dans cette section, on notera cl(A) l'adhérence, int(A) l'intérieur « ordinaire », ir(A) l'intérieur « relatif ».
On sait que, pour des parties quelconques d'un espace topologique (et sans avoir besoin de chercher des contre-exemples bien compliqués), il faut accumuler pas moins de quatre opérateurs pour arriver à des formules justes :
- cl(int(cl(int(A)))) = cl(int(A)) et int(cl(int(cl(A)))) = int(cl(A)).
Les choses se stabilisent beaucoup plus vites pour des convexes, comme l'exprime le théorème ci-dessous et son corollaire :
Théorème — Soit C un convexe dans un espace vectoriel topologique. On suppose en outre C d'intérieur non vide. Alors int(cl(C)) = int(C) et cl(int(C)) = cl(C).
Corollaire — Pour un convexe non vide C en dimension finie, ir(cl(C)) = ir(C) et cl(ir(C)) = cl(C). En particulier les trois convexes emboîtés ir(C), C et cl(C) ont la même frontière relative.
La preuve peut se fonder agréablement sur le lemme suivant :
si
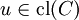

![]u,v]\subset\mathrm{int}(C)](https://static.techno-science.net/illustration/Definitions/autres/a/a2d8ed402f287a7652a91f0a937f8adc_617863fc1ca701caba24e6153189b5d2.png)
dont on ne détaillera pas ici la preuve, facile si on a une bonne intuition graphique du problème.
Montrons par exemple comment la première affirmation se déduit du lemme. L'une des inclusions étant évidente, tout ce qu'il reste à faire est de prouver que tout point x de int(cl(C)) est en fait un point de int(C). Pour ce, on profite de l'hypothèse de non-vacuité de int(C) pour se saisir d'un v auxiliaire lui appartenant. On peut ensuite affiner un ε > 0 suffisamment petit pour que, si on note u = x + ε(x − v) le point u soit dans cl(C). Comme on s'y est pris, x est alors un point du segment ]u,v] auquel le lemme est applicable.
Frontière relative d'un convexe
De même que l'intérieur « ordinaire », la frontière n'est pas toujours un objet pertinent pour l'étude d'un convexe. Ainsi, pour un terrain rectangulaire vivant dans l'espace à trois dimensions, elle est bien décevante puisque égale à toute l'étendue du territoire.
On utilisera plutôt la frontière relative, définie à partir de l'intérieur relatif :
Définition — La frontière relative d'un convexe non vide C dans un espace affine E de dimension finie est le complémentaire de son intérieur relatif dans son adhérence.
Le concept est bien plus satisfaisant : dans l'exemple du terrain, il renvoie bien ce qu'évoque le mot « frontière » du langage courant.
On peut faire la remarque suivante, d'intérêt surtout anecdotique dès lors que le théorème de Krein-Milman en fournit une variante nettement plus puissante :
Proposition — Un convexe compact (non vide et non réduit à un point) est l'enveloppe convexe de sa frontière relative (et a fortiori de sa frontière)
Soit z un point du convexe C. Traçons une droite affine D qui passe par z et qui est incluse dans le sous-espace affine engendré par C. L'intersection
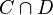
La frontière contenant toujours la frontière relative, l'affirmation a fortiori est alors une évidence.

















































