Adhérence, intérieur et frontière d'un convexe - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Dans le cas particulier de parties convexes d'un espace vectoriel topologique, les opérateurs topologiques élémentaires d'adhérence ou intérieur préservent la convexité. Sous une réserve technique mineure (qui justifie l'introduction de concepts simples, ceux d'intérieur relatif et de frontière relative, qui sont l'intérieur ou la frontière relativement à l'enveloppe affine du convexe), le remplacement d'un convexe par son adhérence ou son intérieur n'en modifie pas profondément la forme ; en particulier le bord du convexe reste discernable sur les nouveaux convexes ouvert ou fermé qu'on lui a substitués.
Observation préalable : le cadre de cet article
Pour des raisons qui tiennent surtout à l'absence de vocabulaire usuel pour les espaces affines munis d'une topologie compatible avec leur structure géométrique, les résultats ci-dessous sont énoncés dans le contexte d'un « espace vectoriel topologique ». Dans les faits, c'est la structure affine de l'espace sous-jacent qui fait sens et tout ce qui est énoncé est valable à l'identique sous l'hypothèse qui serait bien lourde à énoncer d'un « espace affine dont l'espace vectoriel sous-jacent est muni d'une structure d'espace vectoriel topologique ».
En particulier, tout ce qui est écrit est valable dans le cadre des espaces affines de dimension finie. Le lecteur mal à l'aise en topologie générale mais au fait du vocabulaire de base concernant les espaces métriques pourra lire l'article en se restreignant mentalement à un tel cadre, suffisant pour survoler l'essentiel du contenu.
Les espaces sont toujours implicitement réels (il faudrait adapter certaines affirmations relatives aux dimensions dans le cas d'espaces vectoriels complexes).
Intérieur et intérieur relatif d'un convexe
Après s'être intéressé à l'adhérence d'un convexe, il est naturel d'examiner son intérieur. Or il apparaît ici une désagréable dissymétrie : alors que le remplacement d'un convexe C par son adhérence conserve une partie significative de l'information sur la forme de celui-ci (ainsi, du moins en dimension finie, l'adhérence n'est qu'exceptionnellement l'espace ambiant E tout entier, en fait dans le seul cas dégénéré où C = E) le remplacement par l'intérieur peut effacer toute information (l'intérieur étant souvent vide).
On a le choix entre deux solutions, plus ou moins adaptées selon le cas, pour contourner cet obstacle : l'une est de se restreindre dans les énoncés à des convexes dont l'enveloppe affine est l'espace ambiant tout entier —mais dans certains contextes, ce n'est guère pratique, par exemple si on veut évoquer les faces d'un polyèdre— ; l'autre est d'introduire un vocable supplémentaire :
Définition — L'intérieur relatif d'un convexe non vide C dans un espace vectoriel topologique E est l'intérieur de C relativement au sous-espace affine engendré par C.
Comme pour l'adhérence, on a :
Proposition — Dans un espace vectoriel topologique, l'intérieur et l'intérieur relatif d'un convexe sont convexes.
Vu la définition de l'intérieur relatif, il suffit de vérifier l'affirmation pour l'intérieur topologique usuel, dont l'intérieur relatif n'est qu'une manifestation.
Version simplifiée, valable dans le cadre d'un espace vectoriel normé
Notons C le convexe, et soit x et y deux points de
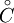
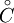
Soit maintenant z un point du segment [x,y] qui peut donc être écrit sous la forme z = λx + (1 − λ)y pour un certain λ de [0,1]. Le cas où z = y se traitant de manière triviale, on peut supposer que
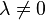
On vérifie alors sans mal que la boule ouverte B(z,λε) est incluse dans C (pour qui veut les détails, un point de cette boule peut s'écrire z + u pour un vecteur u avec
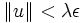
![[x+{1\over\lambda}u,y]](https://static.techno-science.net/illustration/Definitions/autres/2/2779b73edbf275ec9693f120efabd1f1_cb48c5bddcb088e515df4b4ff9a77563.png)
Le point z est donc intérieur à C.
Cas général Il n'y a presque rien à changer : au lieu d'introduire un ε > 0, on introduit un voisinage de 0 noté U de sorte que x + U se susbtitue à B(x,ε). Autour de z, c'est alors le voisinage z + λU qui jouera le rôle que jouait B(z,λε) dans la version précédente.
En dimension finie tout au moins, et contrairement à l'intérieur, l'intérieur relatif d'un convexe non vide n'est jamais vide :
Proposition — En dimension finie, l'intérieur relatif d'un convexe C non vide n'est pas vide, et a la même dimension que C.
Notons d la dimension de C et F le sous-espace affine de dimension d engendré par C.
Il existe alors un d + 1-uplet de points de C constituant un repère affine de F. L'ensemble des points à coordonnées barycentriques toutes strictement positives dans ce repère affine fournit alors la clé de la preuve : il n'est évidemment pas vide, et on vérifie facilement que tous ses points sont dans l'intérieur relatif de C tout en étant assez nombreux pour engendrer affinement F ; le sous-espace affine engendré par l'intérieur relatif de C est donc bien au moins aussi gros que celui engendré par C, d'où l'égalité des dimensions.
En guise de résumé de cette section, on peut faire un bilan rapide, C désignant un convexe non vide d'un espace affine réel E de dimension finie, on a l'alternative suivante :
- ou bien
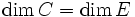
- ou bien