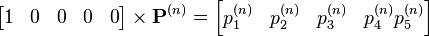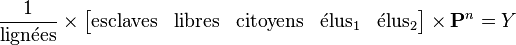Chaîne de Markov - Définition

Illustration de l'impact du modèle

L'exemple qui suit a pour but de montrer l'importance de la modélisation du système. Une bonne modélisation permet de répondre à des questions complexes avec des calculs simples.

On étudie une civilisation (fictive) constituée de plusieurs classes sociales, et dans laquelle les individus peuvent passer d'une classe à l'autre. Chaque étape représentera un an. On considérera une lignée plutôt qu'un individu, pour éviter d'obtenir des citoyens bicentenaires. Les différents statuts sociaux sont au nombre de quatre :

• esclave ;
• libre ;
• citoyen ;
• haut-fonctionnaire.

Dans cette société :

• les esclaves peuvent rester esclaves ou devenir des hommes libres (en achetant leur liberté ou en étant affranchis généreusement par leur maître) ;
• les hommes libres peuvent rester libres ou bien vendre leur liberté (pour payer leurs dettes, etc.) ou encore devenir citoyens (là encore par mérite ou en achetant le titre de citoyen) ;
• les citoyens sont citoyens à vie et transmettent leur citoyenneté à leur lignée (on pourrait croire que le nombre de citoyens tend à augmenter et qu'au bout d'un certain temps, tous sont citoyens mais historiquement, dans les civilisations qui suivaient ce schéma, les citoyens sont décimés par les guerres et de nouveaux esclaves arrivent régulièrement de l'étranger). Ils peuvent aussi se porter candidats lors des élections annuelles afin de devenir hauts-fonctionnaires (magistrats). Au terme de leur mandat, ils peuvent être réélus ou redevenir de simples citoyens.

Pour compliquer un peu l'exemple et montrer ainsi l'étendue des applications des chaînes de Markov, nous considérerons que les fonctionnaires sont élus pour plusieurs années. Par conséquent, l'avenir d'un individu fonctionnaire dépend du temps depuis lequel il est fonctionnaire. Nous sommes donc dans le cas d'une chaîne de Markov non homogène. Heureusement, nous pouvons aisément nous ramener à une chaîne homogène. En effet, il suffit de rajouter un état artificiel pour chaque année du mandat. Au lieu d'avoir un état 4 : Fonctionnaire, nous aurons un état :

• 4 : Fonctionnaire en début de mandat ;
• 5 : Fonctionnaire en seconde année de mandat ;
• etc.

Les probabilités reliant deux états artificiels consécutifs (troisième et quatrième année par exemple) sont de valeur 1 car l'on considère que tout mandat commencé se termine (on pourrait modéliser le contraire en changeant la valeur de ces probabilités). Fixons la durée des mandats à deux ans, le contingent des fonctionnaires étant renouvelable par moitié chaque année. On a alors le graphe suivant :

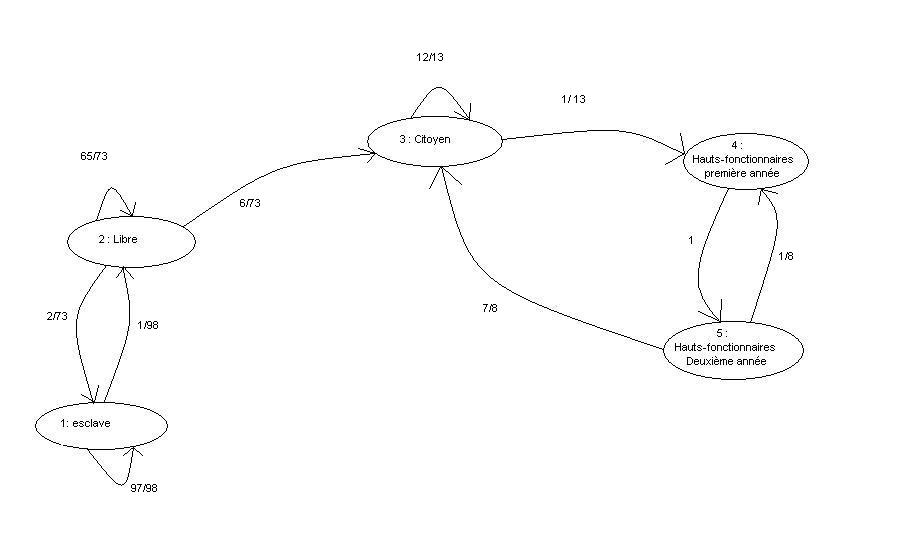
Pour modéliser des élections qui ne seraient pas annuelles, il faudrait de même ajouter des états fictifs (année d'élection, un an depuis la dernière élection, etc.).

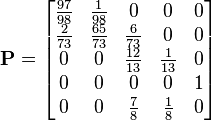
La matrice P s'écrit alors :

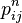
Comme cela est expliqué plus haut, Pⁿ donne les probabilités de transition en n étapes. Donc est la probabilité d'être dans l'état j au bout de n années pour une lignée partie de la classe sociale i. Pour savoir ce que devient un esclave au bout de n ans, il suffit donc d'écrire :

Où est la probabilité d'être dans la classe sociale i au bout de n années sachant que la lignée étudiée est partie de l'état d'esclave.

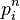
Si on connaît les effectifs de chaque classe sociale à l'an 0, il suffit alors de calculer :

On obtient ainsi la répartition de la population dans les différentes classes sociales (au bout de n années). En multipliant ce vecteur Y par l'effectif total de la population, on obtient les effectifs de chaque classe au bout de n années.

Posons-nous maintenant la question suivante : « Au bout de n années, combien de lignées auront déjà eu un haut fonctionnaire ayant terminé son mandat ? »

La réponse est différente du nombre de mandats effectués en n années car il y a possibilité d'être réélu. Répondre à cette question semble difficile (encore faudrait-il que ce soit possible). En fait, il suffit de changer la modélisation du problème. Passons donc à une nouvelle modélisation pour répondre à cette question. (Par contre, elle ne permet pas de répondre aux questions précédentes d'où la présentation des deux modèles.)

Il suffit de modifier ainsi le graphe :

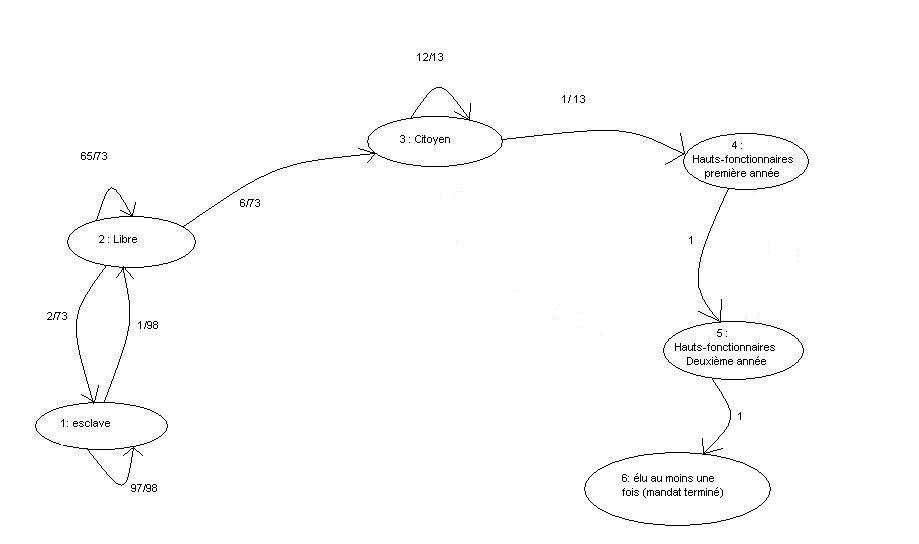
On ajoute un sommet absorbant car une fois qu'une lignée a fini un mandat, on ne tient plus compte d'elle.

Si certains lecteurs font preuve d'esprit critique, ils diront peut-être que le modèle est faux car les lignées comportant un élu ne participent plus aux élections. Il n'en est rien. En effet, le nombre d'élus est proportionnel au nombre de citoyens. Ne pas réinjecter les anciens hauts-fonctionnaires parmi les candidats ne change donc en rien la probabilité pour un citoyen d'être élu car, la population des citoyens étant plus restreinte, le nombre de postes offerts l'est aussi. Ce modèle permet de répondre avec exactitude à la question posée.

On a donc une nouvelle matrice de transition :

En faisant les mêmes calculs qu'aux questions précédentes on obtient en dernière ligne du vecteur solution le pourcentage de lignées ayant accompli au moins un mandat ou bien l'effectif (si on multiplie par l'effectif total de la population). Autrement dit, modéliser à nouveau le problème permet de répondre à la question qui semblait si compliquée par un simple calcul de puissances d'une matrice.