Construction de l'anneau des polynômes - Définition
La liste des auteurs de cet article est disponible ici.
Construction
A désigne un anneau (unitaire) commutatif.
Polynôme
Avec la logique du préambule, un polynôme est défini de la manière suivante :
Polynôme à une indéterminée à coefficients dans A — Un polynôme est une suite à valeurs dans A et nulle à partir d'un certain rang.
Un polynôme P est ainsi, dans le cas général, une suite (p0, p1, p2,..., pk,...) d'éléments de A, que l'on note aussi (p k). Nulle à partir d'un certain rang signifie qu'il existe un entier N tel que si n est plus grand que N, alors pn est égal à 0.
L'ensemble de tous les polynômes ainsi défini est alors noté A[X].
On dispose d'une première propriété, correspondant à une tautologie de la définition :
Égalité entre deux polynômes — Deux polynômes sont égaux si, et seulement si, les suites de leurs coefficients sont égales.
Polynômes particuliers (monômes)
La suite nulle est appelée polynôme nul.
Un monôme est un polynôme dont tous les coefficients sont nuls, sauf, au plus, l'un d'entre eux. Un monôme non nul, correspondant à la suite nulle (0,0,...) sauf en un unique indice k, est appelé monôme de degré k. Cette seule valeur non nulle de la suite est appelée coefficient du monôme de degré k.
Le monôme (0,0,0,..., pk,0,0,...) de degré k est appelé monôme de degré k du polynôme (p0, p1, p2,..., pk,...). Le monôme non nul et de plus grand degré d'un polynôme est appelé monôme dominant et si le monôme dominant possède un coefficient égal à 1, le polynôme est dit unitaire.
Addition et multiplications
A l'image des ensembles de nombres, l'intérêt des polynômes réside dans l'existence d'une addition et d'une multiplication. Ces opérations correspondent à la description du préambule. De manière formelle, l'addition se définit par :
Addition des polynômes — La somme de deux polynômes est égale à la suite dont la valeur indexée par k est la somme des deux coefficients des deux polynômes indexés par k.
![\forall P,Q \in \mathbb A[X] \quad P = (p_0, p_1, p_2,\cdots, p_k,\cdots),\; Q = (q_0, q_1, q_2,\cdots, q_k,\cdots)](https://static.techno-science.net/illustration/Definitions/autres/f/fab9d1617a3f122dc0ce19ce30ccf4d7_7a465d97eef445810ecb5876952b9c89.png)

Pour vérifier que la somme est bien définie, il faut s'assurer que la suite P + Q est bien nulle à partir d'un certain rang, Si la suite définissant P est nulle à partir du rang m et si celle définissant Q est nulle à partir du rang n, on remarque bien que la suite définissant P + Q est nulle à partir du rang le maximum de m et de n.
Il existe deux multiplications, la première est dite externe et correspond à la multiplication d'un nombre élément de A et d'un polynôme. Elle ressemble en cela à la multiplication d'un vecteur par un scalaire.
Multiplication scalaire — La multiplication scalaire d'un élément a de A par un polynôme est la suite dont valeur indexée par k est le produit de a par le coefficient du polynôme indexé par k.
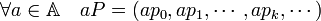
De même que l'addition des polynômes correspond à l'addition des suites, la multiplication scalaire correspond à la multiplication scalaire des suites. Il est une fois encore aisé de vérifier que le résultat est encore une suite nulle, à partir d'un certain rang.
La deuxième multiplication correspond au produit de deux polynômes. Elle est calquée sur le produit décrit dans le préambule :
Produit de polynômes — Soient P égal à (p k) et Q égal à (q l) deux polynômes à coefficients dans A, le produit P.Q est le polynôme défini par :
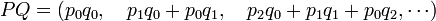
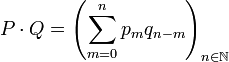
Une observation attentive montre que cette définition correspond exactement au calcul du préambule. Le coefficient d'indice 0 de A.B est le produit des coefficients d'indice 0 de A et de B. Le coefficient d'indice 1 de A.B est la somme de deux termes, le produit du coefficient d'indice 0 de A et du coefficient d'indice 1 de B pour le premier; le produit du coefficient d'indice 1 de A et du coefficient d'indice 0 de B pour le second. Une fois encore les deux définition concordent. Il en est de même pour tous les coefficients.
Vérifier que le produit est bien une suite nulle à partir d'un certain rang n'est pas très difficile. Si la suite P est nulle à partir du rang p, que la suite Q est nul à partir du rang q et que r est un entier plus grand que p + q, le coefficient d'indice r dans la suite P.Q est une somme de produits dont un (au moins) des facteurs est toujours nul, ce qui montre que le polynôme P.Q est une suite nulle à partir de l'indice p + q.

















































