Construction de l'anneau des polynômes - Définition

Indéterminée

On dispose de deux notations différentes pour les polynômes, soit à l'aide du symbole X, soit par les suites. Une unique définition permet de rendre ces deux notations cohérentes. Elle concerne l'objet symbolisé par la lettre X :

Avec cette définition, si n est un entier strictement positif, la suite nulle partout, sauf pour l'indice n où elle vaut 1, est égal à Xⁿ, d'après la règle de multiplication de l'anneau. Pour généraliser cette propriété, on définit le polynôme X⁰ comme étant égal à la suite nulle partout, sauf pour l'indice 0 où elle vaut 1. Ce qui permet de disposer de la règle :

.

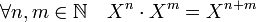
Considérons le polynôme A du préambule, il correspond à la suite (1,0,1,1,0,1,0,...), on peut l'écrire de la manière suivante :

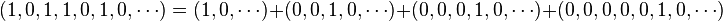
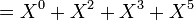
Dans le cas général, un polynôme P, égal à (p₀, p₁, p₂,..., p_n,0 ,...) s'écrit de manière équivalente :

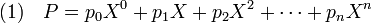
Avec cette nouvelle définition, un monôme est un polynôme de la forme a.Xⁿ, où a est un élément de A appelé coefficient du monôme et n un entier positif, appelé degré du monôme.

L'ensemble A[X] ressemble maintenant à celui couramment utilisé en mathématique et appelé anneau des polynômes. La lettre X symbolise maintenant un objet rigoureusement défini.

La définition de l'indéterminée diffère selon le contexte. On en trouve une plus générale dans l'article polynôme en plusieurs indéterminées. Si la définition de l'indéterminée pour les séries formelles est analogue à celle présentée ici, les analystes utilisent parfois une convention différente, l'indéterminée est la lettre X et selon les besoins, cette lettre désigne soit le polynôme formel décrit ici, soit la variable x qui transforme l'objet série formelle en une fonction analytique.

Polynômes constants

La notation (1), n'est pas totalement usuelle. En général, on ne trouve pas le facteur X ⁰ dans l'expression d'un polynôme. Pour comprendre pourquoi il peut-être omis, il est nécessaire d'étudier l'application φ de A dans A[X], qui à « a » associe le polynôme « a.X⁰ ». Un peu de vocabulaire est utile :

L'application φ est ainsi une application de A dans l'ensemble des polynômes constants de A[X]. Elle possède de nombreuses propriétés, tout d'abord c'est une bijection, c'est-à-dire qu'à un élément de A est associé un unique polynôme constant par φ et à un polynôme constant il existe un unique élément de A d'image ce polynôme constant. Au sens ensembliste, A et les polynômes constants sont deux ensembles copie l'un de l'autre.

L'ensemble des polynômes constants muni de l'addition et de la multiplications des polynômes est un sous-anneau (unitaire) de l'anneau des polynômes. L'addition de A est transportée par l'application φ, c'est-à-dire :

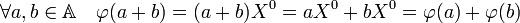
Il en est de même pour la multiplication, ainsi les structures (A, +, .) et l'ensemble des polynômes constants muni des mêmes opérations, sont des copies l'une de l'autre. L'unité 1 de A est envoyée sur l'unité 1X⁰. On parle d'isomorphisme d'anneaux.

L'élément neutre 0 pour l'addition de A est aussi l'élément neutre de A[X] pour l'addition des polynômes, il en est de même pour l'élément neutre 1 de la multiplication de A. Enfin, la multiplication externe de a par un polynôme P donne le même résultat que le produit de a.X⁰ par le polynôme P.

Ces différentes raisons autorise à identifier A avec l'ensemble des polynômes constants. Cela revient à considérer que A[X] contient l'ensemble de nombre A et l'ensemble de nombres A est vu comme constitué des polynômes constants. Cette identification revient à dire que le polynôme X⁰ est égal à 1. On trouve maintenant exactement la notation habituelle :

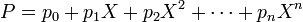
L'ensemble des polynômes A[X] correspond bien à celui décrit dans l'introduction, connu depuis Viète, le mathématicien du XVI^e siècle qui utilise pour la première fois le terme de polynôme. Sa construction est maintenant exposée rigoureusement.