Construction de l'anneau des polynômes - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés élémentaires
Une telle construction ne possède d'intérêt que si l'ensemble obtenu est riche en propriétés, ce qui est le cas. Ici ne sont présentées que les propriétés élémentaires de l'ensemble des polynômes, l'article polynôme formel synthétise les propriétés essentielles.
Structure d'anneau
Un ensemble de nombres, que ce soit celui des entiers, des rationnels, des réels ou des complexes, possède toujours des propriétés communes. Elles sont rassemblées pour décrire une structure générique, caractérisant la catégorie des anneaux commutatif unitaires et intègres.
L'addition des polynômes possède les propriétés suivantes :
Addition — L'ensemble des polynômes à coefficients dans A possède un élément neutre 0 pour l'addition, tout élément possède un opposé, l'addition est associative et commutative. Ces propriétés confèrent à l'ensemble des polynômes muni de l'addition une structure de groupe abélien.
Ces propriétés sont simples à établir. En fait, tout ensemble de suites à valeurs dans un groupe abélien possède une structure de groupe abélien.
La multiplication est un peu moins riche :
Multiplication — L'ensemble des polynômes à coefficients dans A possède un élément neutre 1 pour la multiplication, la multiplication est associative et commutative. Enfin, la multiplication est distributive sur l'addition.
La multiplication est un peu moins riche car tout élément non nul ne possède pas nécessairement un inverse, ainsi le polynôme X ne possède pas d'inverse. Ces différentes propriétés permettent d'établir :
Anneau — L'ensemble A[X] des polynômes en une indéterminée et à coefficients dans A possède une structure d'anneau commutatif unitaire. Cet anneau est intègre si A est intègre : si P et Q sont des polynômes, P.Q est le polynôme nul si, et seulement si, P ou Q est nul.
Degré et valuation
Un indicateur important du polynôme est son degré :
Degré d'un polynôme — Le degré d'un polynôme est le degré de son monôme dominant si le polynôme est non nul et moins l'infini sinon. Autrement dit, si le polynôme P (p0, p1, p2,..., pk,...) n'est pas nul, le degré est égal à l'entier n tel que pn soit le coefficient non nul d'indice le plus élevé :
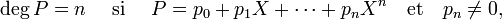
Si le polynôme est nul, on pose
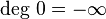
La définition de la somme et du produit des polynômes montre que :
Propriétés du degré — Si l'anneau A est intègre, le degré du produit de deux polynômes de degrés respectifs n et m est égal à la somme n + m. Le degré de la somme de deux polynômes de degrés respectifs n et m est inférieur ou égale au maximum de n et de m.
On remarque par exemple que le coefficients du monôme dominant du produit de deux polynômes non nuls est le produit des deux coefficients des monômes dominants des deux polynômes. Ce qui montre que si P et Q sont deux polynômes non nuls, P.Q est encore un polynôme non nul, autrement dit l'anneau A[X] est intègre. On remarque encore que le produit d'un polynôme non nul par X est toujours un polynôme de degré au moins 1, le polynôme X n'est donc pas inversible.
Valuation d'un polynôme — La valuation d'un polynôme est le degré de son monôme non nul de plus petit degré, si le polynôme est non nul, et plus l'infini sinon. Autrement dit, si le polynôme P (p0, p1, p2,..., pk,...) n'est pas nul, la valuation est égale à l'entier m tel que pm soit le coefficient non nul d'indice le moins élevé :
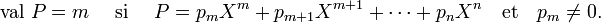
Si le polynôme est nul, on pose val
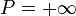
On dispose de propriétés équivalentes pour les valuations :
Propriétés de la valuation — Si l'anneau A est intègre, la valuation du produit de deux polynômes de valuations respectives n et m est égal à la somme n + m. La valuation de la somme de deux polynômes de valuation respectives n et m, est supérieure ou égale au minimum de n et de m.
Il existe en algèbre une définition de la valuation un peu différente et plus générale. La valuation spécifique définie dans ce paragraphe devient avec l'autre définition une valuation particulière.
Une des conséquences de ces deux applications, degré et valuation, est l'existence de deux divisions dans l'anneau des polynômes à coefficients dans un corps (c'est-à-dire si tous les éléments non nuls de A sont inversibles). L'une est dite "euclidienne" et l'autre "selon les puissances croissantes". Elles sont traitées dans l'article Division d'un polynôme.

















































