Endomorphisme de Frobenius - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus précisément en théorie des anneaux, l'endomorphisme de Frobenius, nommé ainsi en l'honneur de Georg Ferdinand Frobenius, est un endomorphisme d'anneau défini de façon naturelle à partir de la caractéristique.
Il est particulièrement utilisé dans le contexte de la théorie de Galois, soit dans le cas des corps de caractéristique non nulle et plus spécifiquement dans le cas des corps finis et dans la théorie des corps de classe. Si le corps est fini, il s'agit alors d'un automorphisme.
Il est généralement utilisé en théorie algébrique des nombres, par exemple pour la démonstration de la loi de réciprocité quadratique.
Définition
Soit A un anneau commutatif unitaire ayant pour caractéristique un nombre premier  . L'endomorphisme de Frobenius est l'application définie par:
. L'endomorphisme de Frobenius est l'application définie par:
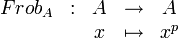
Elle est souvent notée Frob s'il n'y a pas d'ambiguïté et FrobA dans le cas contraire.
- Un élément de Frobenius est une puissance de l'endomorphisme de Frobenius pour la loi de composition des applications.
- L' automorphisme de Frobenius désigne l'endomorphisme de Frobenius s'il est bijectif.
Si l'endomorphisme de Frobenius est bijectif, il en est de même pour chaque élément de Frobenius, l'ensemble des éléments forment alors un sous-groupe du groupe des bijections de l'anneau, d'où la définition suivante:
- Dans le cas de la bijection, le groupe de Frobenius est l'ensemble des éléments de Frobenius munis de la loi de composition des applications.
Applications
Les applications sont nombreuses, l'endomorphisme de Frobenius apparaît comme un outil indispensable pour l'analyse des anneaux commutatifs unitaires intègres de caractéristique p si p est premier. On peut citer comme exemple l'analyse de la séparabilité ou encore celles des polynômes minimaux dans un corps fini.
Polynôme et séparabilité
L'objet est ici de démontrer le théorème :
- Un corps commutatif de caractéristique p est parfait si et seulement si son endormorphisme de Frobenius est bijectif.
et son corollaire, dû au fait que l'endomorphisme de Frobenius est bijectif sur tout corps fini, et que de plus un tel corps est commutatif d'après le théorème de Wedderburn :
- Tout corps fini est parfait.
On peut remarquer que l'ensemble A[X] des polynômes à coefficients dans A est aussi un anneau commutatif intègre et de caractéristique p. L'application FrobA[X] est donc définie et c'est un endomorphisme injectif d'anneau. Les propriétés de morphisme permettent de déduire la propriété suivante:
![\forall (a_i) \in A^{n+1} \quad Frob_{A[X]}(\sum_{i=0}^n a_i.X^i)=\sum_{i=0}^n a_i^p.X^{pi}\;](https://static.techno-science.net/illustration/Definitions/autres/0/05863f309a88baff2c3d9837cf76f5f3_e12663df5b67f3badd3be73ae235cfb5.png)
Si A est le corps premier
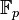
![\forall P[X] \in \mathbb F_p[X] \quad Frob _{\mathbb F_p[X]}(P[X])=P[X^p]\;](https://static.techno-science.net/illustration/Definitions/autres/6/62d7891a398ed22e7705aabdb348f9d2_d879ef80dd06f91cc2bdf1b611fa05f8.png)
L'endomorphisme de Frobenius n'est pas surjectif car l'ensemble d'arrivée ne contient que des termes en puissance de p.
L'endormorphisme de Frobenius sur les polynômes permet d'analyser la séparabilité des polynômes. Un polynôme est dit séparable s'il n'admet pas de racine multiple dans son corps de décomposition. Or un polynôme irréductible n'est séparable que si sa dérivée formelle est non nulle. Dans un anneau de caractéristique p, cette proposition, démontrée dans l'article Extension séparable se traduit par :
- Un polynôme irreductible P[X] est séparable si et seulement s'il n'existe pas de polynôme Q[X] dans A[X] tel que l'on ait l'égalité P[X]=Q[Xp].
En effet, si le polynôme Q[X] existe avec la propriété de l'énoncé, alors la dérivée de P[X] vérifie l'égalité suivante :
![P'[X]=p.Q'[X^p].X^{p-1}\;](https://static.techno-science.net/illustration/Definitions/autres/f/fd17e089835088837d6dd705bc9cb995_d435a89dd50e5b22a27ce26b2a47098e.png)
Comme A est de caractéristique p, le polynôme dérivé est nul et P[X] n'est pas séparable. Ce calcul montre en particulier qu'aucun polynôme dérivé n'a de terme non nul de degré pk-1, pour k entier. Réciproquement si P[X] n'est pas séparable, alors P' [X] n'est pas nul, donc il existe un degré i, non multiple de p par la remarque précédente, tel que le coefficient ai du terme de degré i-1 est non nul, et, par intégration, P[X] a un terme de degré i non nul. Puisque i n'est pas multiple de p, on a la non existence voulue.
On remarque ensuite que si l'endomorphisme de Frobenius sur A est bijectif, alors tous les polynômes de la forme Q[Xp] admettent un antécédent par l'endomorphisme sur A[X].
- Si l'endormorphisme de Frobenius est bijectif, alors l'ensemble des polynômes non séparables est l'ensemble d'arrivée de l'endomorphisme. En particulier, tous ces polynômes sont des puissances pèmes et donc ne sont pas irréductibles sur A[X].
On a ainsi montré que si un corps de caractéristique p admet un endomorphisme de Frobenius bijectif, alors tous les polynômes irréductibles sur ce corps sont séparables, et donc le corps est parfait.
Réciproquement, si l'endomorphisme de Frobenius n'est pas surjectif sur un corps K, il existe un élément a qui ne possède pas de racine pieme. Considérons le polynôme P[X]=Xp-a. Soit L le corps de rupture sur K de P[X] et r sa racine. Comme la dérivée formelle de P[X] est nulle, la racine est une racine multiple d'ordre p, et donc le polynôme n'est pas séparable. Montrons que P[X] est irréductible. Soit D[X] un diviseur irréductible de P[X] dans l'anneau K[X]. On a alors D[X]=(X-r)k dans L[X] pour un certain entier k, qui ne peut être égal à 1, sinon la racine r de a est dans K, et c'est une contradiction ; et D[X] n'est donc pas séparable. Alors la première proposition du paragraphe garantit l'existence d'un polynôme Q[X] tel que D[X]=Q[Xp], et donc, son degré k est un multiple de p, d'où k=p, ce qui est le résultat attendu : il existe donc une extension L contenant un élément non séparable.
Polynôme minimal et corps fini
Dans le cas des corps finis, l'automorphisme de Frobenius permet la détermination de tous les polynômes minimaux. Dans ce paragraphe, le corps considéré est
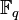
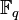
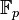
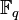
L'automorphisme Frobn est égal à l'identité, ce qui montre que le polynôme Xq - X a pour racines tous les éléments de
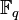
- Chaque polynôme minimal d'un élément
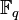
La définition suivante permet d'affiner l'analyse :
- Deux éléments de
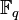
La conjugaison apparaît comme une classe d'équivalence sur
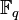
![\forall P[X] \in \mathbb F_p[X] \; \forall l \in \mathbb Z \quad Frob^l (P[X])=P[Frob^l(X)]](https://static.techno-science.net/illustration/Definitions/autres/8/88506cd0ad5b1ac7dc5e1ffbbbdf6d4d_ed4bdab39fbe47bc63c07df3d20bebee.png)
On en déduit que l'image d'une racine d'un polynôme minimal M[X] par un élément de Frobenius est une racine de M[X]. Réciproquement l'image d'une racine par un élément de Frobenius est annulée par M[X], et M[X] est un polynôme irréductible unitaire. En conclusion, les classes de conjugaisons sont les ensembles constitués par les différentes images d'un élément par les itérés du groupe de Frobenius.
- Les classes d'équivalences de la relation de conjugaison sont les orbites de l'action de groupe du groupe des éléments de Frobenius.
Il devient alors possible de déterminer exactement le nombre de polynômes minimaux pour de degré n ainsi que le nombre de polynômes primitifs, c’est-à-dire les polynômes dont les racines engendrent toute le groupe multiplicatif du corps. Un élément a de
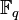
![\mathbb F_p[a]](https://static.techno-science.net/illustration/Definitions/autres/3/3f7c72277ea387941327e9ece31a060d_5f681bc661b4198cfe0119e9f733d83e.png)
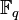
![\mathbb F_p[a]](https://static.techno-science.net/illustration/Definitions/autres/3/3f7c72277ea387941327e9ece31a060d_5f681bc661b4198cfe0119e9f733d83e.png)
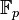
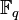
- Soit p un nombre premier et n un entier strictement positif. Le nombre de polynômes à coefficients dans
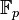
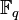
L'article sur les corps finis montre qu'un élément de
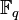
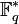
- Soit p un nombre premier et n un entier strictement positif. Le nombre de polynômes à coefficients dans
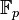
Deux exemples sont donnés dans le paragraphe Polynôme irréductible de l'article corps fini.

















































