Décohérence quantique - Définition

Bibliographie

• Maximilian Schlosshauer ; Decoherence And the Quantum-To-Classical Transition, Springer-Verlag (2007). . Ouvrage de référence sur la décohérence, clair et d'une grande précision.

• Wojciech Hubert Zurek ; Decoherence and the Transition from Quantum to Classical-Revisited, séminaire Poincaré (Paris - 19 novembre 2005). Texte complet disponible aux formats PostScript et pdf ici.

• Hans Dieter Zeh ; Roots and Fruits of Decoherence, séminaire Poincaré (Paris - 19 novembre 2005). Texte complet disponible sur l'ArXiv : quant-ph/0512078.

• Jean-Michel Raimond & Serge Haroche ; Monitoring the Decoherence of Mesoscopic Quantum Superpositions in a Cavity, séminaire Poincaré (Paris - 19 novembre 2005). Texte complet disponible aux formats PostScript et pdf ici.

• Serge Haroche, Jean-Michel Raimond & Michel Brune ; Le chat de Schrödinger se prête à l'expérience - Voir en direct le passage du monde quantique au monde classique, La Recherche 301 (Septembre 1997) 50.

• Serge Haroche ; Une exploration au cœur du monde quantique, dans : Qu'est-ce que l'Univers ?, Vol. 4 de l'Université de Tous les Savoirs (sous la direction d'Yves Michaux), Odile Jacob (2001) 571.

• Roland Omnès ; Comprendre la mécanique quantique, EDP Sciences (2000) . Par un professeur de physique théorique émérite de l'Université de Paris-Sud (Orsay), une discussion de l' interprétation de Copenhague de la mécanique quantique, du problème de la mesure et de la théorie des histoires consistantes de Griffiths et de la décohérence, par l'un de ses pionniers.

• E. Joos, H.D. Zeh, C. Kiefer, D. Giulini, K. Kupsch, I.O. Stamatescu ; Decoherence and the Appearance of a Classical World in Quantum Theory, Springer-Verlag (1996). Deuxième édition (2003)

• Gennaro Auletta ; Foundation & Interpretation of Quantum Mechanics (in the light of a critical - historical analysis of the problems and of a synthesis of the results), Wolrd Scientific (2001) . Par un professeur de l'Université de Rome, un ouvrage monumental (environ 1000 pages) sur les fondements conceptuels de la mécanique quantique des origines à nos jours - y compris les questions de décohérence - mis en relation avec les avancées expérimentales les plus récentes.

• Mario Castagnino, Sebastian Fortin, Roberto Laura and Olimpia Lombardi, A general theoretical framework for decoherence in open and closed systems, Classical and Quantum Gravity, 25, pp. 154002–154013, (2008). Cadre théorique général pour la décohérence, qui comprend les formalismes initialement conçus pour être appliqués des systèmes ouverts ou fermés.

Annexe : Formalisme mathématique de la décohérence

Modèle de décohérence

Soit une boule macroscopique de rayon R, dans un état superposé de positions aux coordonnées x1 et x2.

Son état quantique est ,
et étant respectivement l'état de position x1 et x2. On suppose x1 et x2 assez éloignés, et l'état de position suffisamment centré pour que et soient orthogonaux (aucune influence l'un sur l'autre). Ces deux états peuvent donc appartenir à une base orthonormée. Le processus de décohérence se déroule dans une base privilégiée, qui est la base propre de l'observable ayant une intrication minimale (idéalement, nulle) avec l'environnement : ici la position.

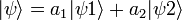
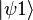
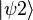
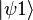
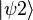
La matrice densité initiale, dans cette base, correspondant à cet état quantique est très simple : .

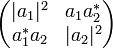
Cette boule est plongée dans un environnement constitué de particules d'impulsion moyenne p, dont la distribution de vitesse (direction) est aléatoire (typiquement, une atmosphère, ou un éclairage non cohérent et non monochromatique).

Soit une particule d'impulsion p, venant heurter en x la boule dans l'état x1. Sa fonction d'onde est . Après le choc, considéré comme élastique, on peut démontrer que la fonction d'onde de la particule devient .

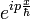
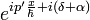
On constate donc un déphasage de la fonction d'onde de l'environnement à chaque fois qu'une collision se produit. Ces déphasages s'accumulent au cours du temps, donnant une évolution dynamique de la matrice densité :

, avec .

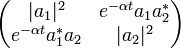
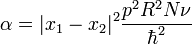
Quand t augmente, la matrice densité tend rapidement vers la forme . On parle alors de diagonalisation de la matrice. Cet état diagonal est caractéristique d'états quantiques orthogonaux, et donc mutuellement exclusifs.