Degré (angle) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un degré, généralement représenté par ° (le symbole degré), est une mesure d'un angle plan, qui représente le 1⁄360e d'un tour complet ; un degré est aussi équivalent à π/180 radians. Lorsque cet angle est en rapport avec un méridien de référence, il indique un emplacement le long d'un grand cercle d'une sphère, comme la Terre (voir Coordonnées géographiques), Mars ou la sphère céleste.
Historique et généralités
Le degré, divisé en minutes et secondes qui sont des soixantièmes, vient des Babyloniens, qui comptaient en base 60 (sexagésimale). Les mathématiciens arabes ont poursuivi et mesuré les angles célestes et terrestres de la même manière. La mesure du temps de cette façon, directement issue des angles astronomiques, en a découlé.
L’utilité originelle des 360° du système sexagésimal est de faciliter le calcul des fractions (et des multiplications). En effet, 360 étant le multiple de (1 × 2 × 3 × 4 × 5) x 3, il se divise donc par ces multiples ainsi que par 6, 8, 9, 10, 12, 15, etc. c’est-à-dire toutes les combinaisons de ces multiples.
Ainsi : 3⁄5 - 1⁄3 = 9⁄15 - 5⁄15 = 4⁄15 correspond à 216° - 120° = 96° ce qui est plus aisément calculable sans calculateur que 0,6 - 0,333… = 0,266… Avec une légère familiarisation, et cela tout en se passant de la méthode du commun dénominateur, on s’aperçoit que le résultat 96° = 4 × 24° soit quatre quinzièmes. Une approche alternative aura aussi donné à voir que 90° + 6° est égal à un quart plus un soixantième, ou encore 60° + 36°, soit un sixième plus un dixième.
| n | 2 | 3 | 4 | 5 | 6 | 15/2 | 8 | 9 | 10 | 45/4 | 12 | 15 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 360° / n | 180 | 120 | 90 | 72 | 60 | 57 | 45 | 40 | 36 | 32 | 30 | 24 | 20 |
| 60' ou " / n | 30 | 20 | 15 | 12 | 10 | 8 | 7.5 | 6.666 | 6 | 5.333 | 5 | 4 | 3.333 |
| n | 2/9 | 1/4 | 4/15 | 3/10 | 1/3 | 3/8 | 2/5 | 5/12 | 4/9 | 7/15 | 8/15 | 5/9 | 7/12 | 3/5 | 5/8 | 2/3 | 7/10 | 11/15 | 3/4 | 7/9 | 4/5 | 5/6 | 7/8 | 8/9 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n360° | 80 | 90 | 96 | 108 | 120 | 135 | 144 | 150 | 160 | 168 | 192 | 200 | 210 | 216 | 225 | 240 | 252 | 264 | 270 | 280 | 288 | 300 | 315 | 320 |
Finalement, du fait que 360° égale 0°, on se retrouve à calculer en modulo 360 lorsque l’on parle en degrés. On peut souvent opérer les calculs dans les modulos inférieurs que sont les multiplicateurs de 360. Au plus simple, sept demi-tours valent un demi-tour. En langage mathématique : 7 ≡ 1 (mod 2), sept est congru à un, modulo deux ; et 7 × 180° = 1260° ≡ 180° (mod 360°). En pratique, on se contente de dire sept fois cent quatre-vingts degrés est égal à cent quatre-vingts degrés. De même 120° + 270° = 390° ≡ 30° (mod 360°).
Mesure d'angle solide
En astronomie de position, le degré carré est utilisé pour mesurer un angle solide sur la sphère céleste. Un degré carré vaut
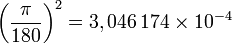
Mesure d'angle plan
Le degré d’arc (symbole °) est une unité pratique d’angle plan. Un angle plat vaut 180°. Bien qu’en dehors du système international (SI), le degré est en usage avec lui.
Un degré vaut π⁄180 radians, 10⁄9 grades ou 160⁄9 mils, soit 1⁄360 d’un tour complet.
Les préfixes du SI sont rarement appliqués aux symboles du degré d’arc et de ses subdivisions (uniquement à la seconde d’arc, en fait) ; ces symboles sont également les seuls à ne pas être séparés du nombre les précédant par une espace : on doit écrire « 12° 30′ » et non « 12 ° 30 ′ ».