Démonstration des lois de Kepler - Définition

Introduction

Les lois de Kepler ont été découvertes à partir des observations de Tycho Brahe à la fin du XVI^e siècle et de leur analyse poussée par Johannes Kepler dans les décennies qui ont suivi.

En 1687 dans les Philosophiae Naturalis Principia Mathematica, Isaac Newton introduit la force de gravitation, qui se veut être à la fois une explication aux mouvements des planètes, et à la pesanteur sur Terre. Le problème exposé ici est de démontrer que la seule expression de la loi universelle de la gravitation, combinée au principe fondamental de la dynamique, fournit une justification des lois empiriques de Kepler. Il fut résolu par Newton.

Une autre démonstration géométrique a été donnée par Richard Feynman, durant ses cours. Il ne l'a pas publiée, mais Brian Beckman l'a fait en 2006 dans "The Journal of Symbolic Geometry", volume 1.

Conventions et notations pour les démonstrations qui vont suivre

Pour simplifier, prenons le Soleil comme origine du référentiel, l'axe z perpendiculaire à la droite passant par le Soleil et la planète et perpendiculaire à la direction de la vitesse de la planète au temps t = 0. L'axe x dans la direction correspondante à la distance la plus petite entre le Soleil et la planète. La distance la plus grande entre le Soleil et la planète sera dans la direction -x.

• la masse du Soleil.
• la masse de la planète.
• la position du Soleil. C'est l'origine du référentiel.
• la position de la planète.
• l'instant où la planète se trouve le plus proche du Soleil.
• la position de la planète au temps .

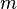
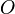
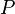
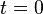
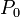
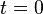
Elle s'appelle le périhélie. C'est le point de la trajectoire près de Hélios; soit le plus proche du Soleil.

• le vecteur allant du Soleil à la planète.
• = la distance du Soleil à la planète.
• le vecteur allant du Soleil à la planète au temps .
• la vitesse de la planète.
• la vitesse de la planète au temps .
• la force d'attraction de la planète par le Soleil.
• le moment cinétique relativement à l'origine où se trouve le Soleil.

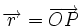
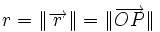
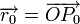
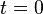
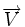
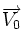
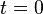
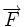
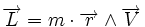
C.f. le produit vectoriel " " pour des informations sur cet opérateur.

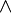
Deuxième loi, loi des aires (1609)

Soit A(t) l'aire de la surface balayée par le rayon vecteur durant le mouvement, alors cette seconde loi stipule que des aires égales sont balayées dans des temps égaux.

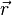
• Démonstration :

En dérivant le moment cinétique par rapport au temps, on obtient :

qui vaut 0.

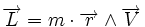
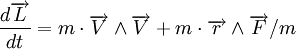
Donc le moment cinétique est un vecteur constant. Cela résulte du fait que la force est centrale (cf. mouvement à force centrale)

D'autre part :

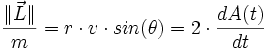
En conséquence :

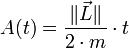
Première partie de la première loi (1609)

Dans un référentiel immobile par rapport au Soleil, la trajectoire d'une planète se trouve dans un plan.

• Démonstration :

Cela résulte du fait que le Soleil attire la planète selon une force centrale. C'est-à-dire une force qui est toujours dirigée de la planète vers le Soleil.

En effet, étant données une position et une vitesse initiales, cela définit un plan. Selon nos conventions ci-dessus, c'est le plan passant par l'origine O, contenant les axes x et y.

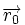
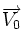
Puisque la force est centrale, elle et l'accélération sont dans une direction se trouvant dans ce même plan. Donc les variations de vitesses et les variations de positions resteront dans ce même plan. En conclusion toute la trajectoire restera dans ce plan.

La deuxième loi de Kepler donnera une deuxième démonstration de cette partie.

Troisième loi (1618)

Le carré de la période varie comme le cube du demi-grand axe  :

s'appelle la constante de Gauss : elle est connue avec une extraordinaire précision, dix chiffres significatifs et vaut 0.01720209895 (alors que n'est connue qu'avec 5 chiffres significatifs).

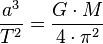
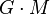
Démonstration :

• En utilisant :   et   ,

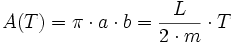
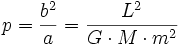
puis en éliminant entre ces égalités, on obtient le résultat annoncé.

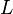
Par conséquent, toutes les ellipses de même grand axe, quelle que soit leur excentricité , ont la même période de révolution jusqu'à la circulaire où .