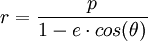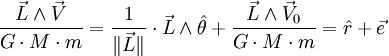Démonstration des lois de Kepler - Définition

Deuxième partie de la première loi (1609)

Dans un référentiel immobile par rapport au Soleil, la trajectoire d'une planète est elliptique, un foyer étant le Soleil. Le Soleil n'est un des foyers qu'approximativement, du fait que sa masse M est très supérieure à celle de la masse m de la planète. Pour être exact, il faudrait se placer au centre de gravité du système Soleil - planète.

• Démonstration :

Ce fait est directement lié au fait que l'hodographe est un cercle dans le cas de l'attraction universelle de Newton.

Le principe fondamental de la dynamique s'écrit :

    où    

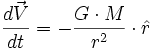
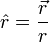
Par changement de variable, on a :

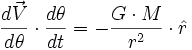
(Attention : L'angle noté θ dans ce paragraphe est différent de celui du paragraphe précédent)

Rappelons l'expression de la loi des aires obtenue au paragraphe précédent :

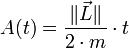
ainsi, l'aire balayée pendant un temps égale . Or cet aire vaut .

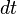
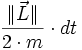
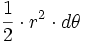
Donc

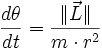
En combinant ces deux relations, on obtient :

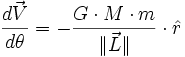
D'où en intégrant par rapport à θ :    car   

= le vecteur unité perpendiculaire à dans le plan de la trajectoire, dirigé dans le sens le plus proche de celui de la vitesse.

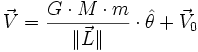
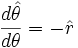
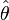
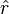
Ce résultat s'appelle : théorème de Hermann, Laplace, Runge, Lenz, Hamilton : cf. vecteur de Runge-Lenz.

L'hodographe est un cercle excentré par rapport à l'origine des vitesses. Il en résulte que la trajectoire est une conique : si l'origine des vitesses est à l'intérieur du cercle, la conique est une ellipse ; si elle est à l'extérieur, c'est une hyperbole ; cas limite : une parabole. Ce théorème de cinématique est très vieux, mais on l'attribue à tort à Hamilton ; il était encore enseigné dans le cours de cosmographie de « math-élem » (terminale S actuelle) : cf. par exemple Lebossé, cours de mathématiques élémentaires. On va en donner la démonstration due à Landau, très algébrique :

Le théorème précédent se réécrit après multiplication vectorielle par et simplifications :

s'appelle le vecteur d'exentricité. On montre qu'il est constant. (C.f. lien externe n°2)

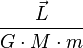
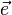
puis en effectuant le produit scalaire avec et en simplifiant :

, avec

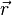
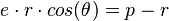
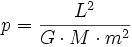
soit

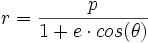
Ce qui est la définition focale d'une conique en coordonnées polaires, d'excentricité et de paramètre , d'angle polaire ayant pour origine le périhélie, comme il est usuel de le faire.

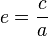
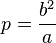
Si on prend l'aphélie comme origine :