Deuxième principe de la thermodynamique - Définition

Historique de la loi

Sadi Carnot (1796–1832)

L'origine de la deuxième loi de la thermodynamique remonte à 1824 et est due au physicien français Sadi Carnot, fils de Lazare Carnot. C'est lui qui, dans le traité Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance (Sadi Carnot utilisait le terme de machine à feu pour désigner les machines thermiques), fut le premier à établir que l'efficacité thermodynamique d'une telle machine dépendait de la différence de température entre la source chaude et la source froide. Bien qu'utilisant le concept dépassé du calorique qui considérait que la chaleur, par analogie avec un fluide, était une substance matérielle qui ne pouvait qu'être soit ajoutée, soit enlevée, soit transférée d'un corps à un autre, il réussit, par une expérience de pensée, à proposer le principe suivant : l'efficacité maximale η d'un moteur ditherme fonctionnant selon le cycle de Carnot avec une source chaude de température T_H (hot) et une source froide de température T_C (cold) vaut :

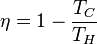
Cette expression de l'efficacité de Carnot correspond au fonctionnement cyclique et réversible d'une machine ditherme. Au cours du cycle, la source chaude à la température T_H fournit la quantité de chaleur Q_H au système moteur. Celui-ci fournit un travail W et restitue une quantité de chaleur Q_C à la source froide de température T_C ( voir figure ).

Comme le fonctionnement est cyclique, l'état final est identique à l'état initial et l'énergie interne U du système reste constante car c'est une Fonction d'état, d'où ΔU = 0 .

Application du premier principe :

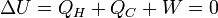
Donc

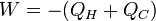
Toujours pour cette évolution cyclique réversible l'application du second principe donne :

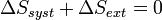
d'où et

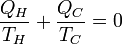
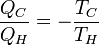
L'efficacité du moteur correspond au rapport du travail fourni (en valeur absolue) sur la chaleur qu'il a reçue de la source chaude

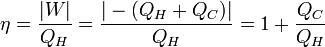
d'où :

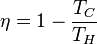
Le cycle de Carnot étant réversible, l'efficacité obtenue est l'efficacité maximale théorique pour un moteur fonctionnant entre ces deux températures. Elle n'est jamais atteinte dans un cycle réel. Dans le cas d'une machine à vapeur d'eau, l'efficacité théorique maximale calculée pour T_H = 373 K et T_C = 298 K , serait égale à η = 0,2.

On retrouve également l'un des énoncés historiques du second principe de la thermodynamique en envisageant le cas où T_H = T_C. Dans ce cas, l'efficacité est nulle et le moteur ne fournit donc aucun travail. Ceci constitue l'énoncé de Thomson du second principe :

« Un système en contact avec une seule source ne peut, au cours d'un cycle, que recevoir du travail et fournir de la chaleur. »

— William Thomson, 1852

Appréciations philosophiques

Dans Identité et réalité (1908), le philosophe des sciences Émile Meyerson propose une analyse du deuxième principe de la thermodynamique.