Deuxième principe de la thermodynamique - Définition

Introduction

Le deuxième principe de la thermodynamique (également connu sous le nom de deuxième loi de la thermodynamique ou principe de Carnot) établit l'irréversibilité des phénomènes physiques, en particulier lors des échanges thermiques. C'est un principe d'évolution qui fut énoncé pour la première fois par Sadi Carnot en 1824. Il a depuis fait l'objet de nombreuses généralisations et formulations successives par Clapeyron (1834), Clausius (1850), Lord Kelvin, Ludwig Boltzmann en 1873 et Max Planck (voir Histoire de la thermodynamique et de la mécanique statistique), tout au long du XIX^e siècle et au-delà.

Le second principe introduit la fonction d'état entropie : S, usuellement assimilée à la notion de désordre qui ne peut que croître au cours d'une transformation réelle.

Énoncé de la loi

Toute transformation d'un système thermodynamique s'effectue avec augmentation de l'entropie globale incluant l'entropie du système et du milieu extérieur. On dit alors qu'il y a création d'entropie.

La fonction d'état entropie : S, a été considérée comme une mesure du désordre.

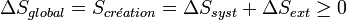
Dans le cas d'une transformation réversible, la création d'entropie est nulle.

Remarques

• L'entropie d'un système isolé ne peut qu'augmenter ou rester constante puisqu'il n'y a pas d'échange de chaleur avec le milieu extérieur.

• L'entropie d'un système peut diminuer mais cela signifie que l'entropie du milieu extérieur augmente de façon plus importante ; le bilan entropique étant positif ou nul si la transformation est réversible.

• L'expression « degré de désordre du système » introduite par Boltzmann peut se révéler ambigüe et subjective. En effet on peut aussi définir l'entropie comme une mesure de l'homogénéité du système considéré. L'entropie d'un système thermique est maximale quand la température est identique en tout point. De même, si on verse un liquide colorant dans un verre d'eau, l'entropie du système coloré sera maximale quand, suite au mélange, la couleur du contenu sera devenue uniforme. Tout système isolé, siège d'une agitation aléatoire, tend spontanément à s'homogénéiser de manière irréversible ce qui intuitivement semble contraire à une augmentation du désordre.

Le second principe est un principe d'évolution qui stipule que toute transformation réelle s'effectue avec création d'entropie.

Notion de réversibilité

Une transformation réversible est une transformation quasistatique susceptible d'être inversée à la suite d'une modification progressive des contraintes extérieures, en permettant au système de retrouver les états antérieurs successifs. En fait cela revient à passer le film de la transformation à l'envers ! Si ce film paraît ridicule c'est que la transformation n'est pas réversible. En réalité, toutes les transformations réelles sont irréversibles. Une transformation réversible représente en effet, le cas limite d'une transformation réelle, conduite d'une manière infiniment lente, constituée d'une suite d'états d'équilibre infiniment voisins et caractérisée par des phénomènes dissipatifs nuls. C'est donc un modèle idéal de transformation.

On peut recenser plusieurs causes d'irréversibilité (liste non exhaustive) :

• inhomogénéité (source de diffusion) : densité moléculaire, température, pression,...
• phénomène dissipatif : frottements fluides et solides
• réorganisation spontanée de la matière : réaction chimique.

Formulations du second principe

Le second principe introduit la fonction d'état extensive S, appelée entropie. La variation d'entropie d'un système, lors d'une transformation quelconque, peut être décrite comme la somme d'un terme d'échange et d'un terme de création :

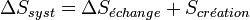
• Le terme de création, toujours positif ou nul, impose le sens de l'évolution de la transformation,  ; l'égalité n'a lieu que pour une transformation réversible.
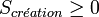
• Le terme d'échange dans le cas d'un système fermé échangeant la quantité de chaleur Q avec le milieu extérieur à la température T est égal à .

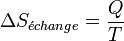
Une autre formulation est possible comme nous l'avons vu précédemment, en considérant l'entropie du système et l'entropie du milieu extérieur. Cette formulation est totalement compatible avec la précédente.

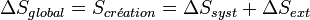
En effet

correspond à l'entropie échangée par le système avec le milieu extérieur. Si l'on se place du côté du milieu extérieur le signe s'inverse d'après la règle des signes et donc :

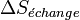
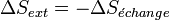
Il s'ensuit

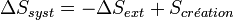
D'où

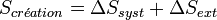
La variation d'entropie globale correspond à l'entropie créée et est égale à la somme des variations d'entropie du système et du milieu extérieur. Elle est toujours positive dans le cas des transformations réelles irréversibles. En revanche dans le cas idéal des transformations réversibles elle est nulle.

Considérons une transformation effectuée soit de façon réversible soit de façon irréversible, à la température T. L'entropie étant une fonction d'état sa variation sera la même pour les deux chemins envisagés. En revanche la chaleur dépendra du chemin suivi car elle n'est pas une fonction d'état.

• Transformation réversible:

puisque l'entropie créée est nulle.

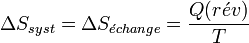
• Transformation irréversible:

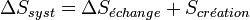
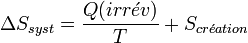
Il s'ensuit que puisque l'entropie créée est positive.

L'expression ainsi obtenue a été formulée par Clausius. On l'appelle encore inégalité de Clausius. C'est une autre façon d'exprimer le second principe.

• Conséquence sur le transfert thermique:

Intuitivement on sait que la chaleur passe d'un corps chaud à un corps plus froid. Le second principe permet de le démontrer. Considérons un système isolé constitué de deux sous-systèmes, syst1 et syst2 dont les températures respectives T1 et T2 sont différentes.

La chaleur échangée par syst1 est Q1 et celle échangée par syst2 est Q2. Comme le système est isolé la chaleur échangée avec le milieu extérieur est nulle, donc Q1 + Q2 = 0 . D'où Q2 = - Q1.

Appliquons le second principe

S_créée = ΔS_syst + ΔS_ext > 0

or ΔS_syst = ΔS_syst1 + ΔS_syst2 et ΔS_ext = 0 puisque le système est isolé.

Il s'ensuit :

S_créée = ΔS_syst1 + ΔS_syst2

ΔS_syst1 = Q1/T1

ΔS_syst2 = Q2/T2 = -Q1/T2

Donc S_créée = Q1/T1 - Q1/T2

S_créée = Q1 (1/T1 - 1/T2)

Comme la transformation est irréversible :

S_créée = Q1 (1/T1 - 1/T2) > 0

Si T1 est supérieure à T2, il faut que Q1 soit négative pour que le bilan entropique soit positif. D'après la règle des signes, cela signifie que le syst1 fournit la chaleur au syst2 qui la reçoit et donc que la chaleur passe du chaud au froid.

En toute rigueur, la température ne change pas brutalement entre les deux sous-systèmes car au voisinage de la frontière, la température varie progressivement entre T1 et T2. On dit qu'il y a un gradient de température ; phénomène intimement lié à la notion d'irréversibilité. Néanmoins ce phénomène ne s'oppose pas à la démonstration précédente démontrant le sens du transit de chaleur. Si les températures T1 et T2 sont très proches l'une de l'autre, on peut considérer que la transformation se rapproche d'une transformation réversible (petit déséquilibre de la variable température) et l'on constate alors que S_créée tend vers zéro.

• Conséquence sur le travail utile fourni par un système:

Le travail ainsi que la chaleur ne sont pas des fonctions d'état et leur valeur dépend de la nature de la transformation affectant le système.

Considérons une transformation effectuée soit de façon réversible soit de façon irréversible à la température T. La variation d'entropie sera la même car l'entropie est une fonction d'état. En revanche, W(rév)≠ W(irrév) et Q(rév)≠ Q(irrév).

ΔS(syst) = Q(rév)/T

ΔS(syst) > Q(irrév)/T

Donc Q(rév) > Q(irrév)

Appliquons maintenant le premier principe

ΔU = W(rév)+ Q(rév) = W(irrév) + Q(irrév)

Il en résulte que : W(rév)< W(irrév)

Or pour un système moteur fournissant du travail, le travail est compté négativement d'après la règle des signes choisie en thermodynamique. Ce qui est important c'est la valeur absolue du travail utile. D'où:

|W(rév)| > |W(irrév)|

Le travail utile fourni par un système moteur est plus important si la transformation est réversible.

Les frottements étant la principale cause d'irréversibilité on comprend pourquoi on essaye de les minimiser par la lubrification.