Deuxième principe de la thermodynamique - Définition

Autres interprétations et conséquences du second principe

Transfert d'extensité

Une autre interprétation, plus « physique » du second principe peut être formulée. En effet, imaginons un cylindre creux fermé hermétiquement aux deux extrémités. Imaginons aussi un piston libre de se déplacer dans ce cylindre. Si l'on déplace le piston vers la gauche, la partie gauche voit sa pression augmenter et son volume diminuer et, vice-versa, la partie droite voit sa pression chuter et son volume augmenter. Si l'on relâche le piston, il va spontanément se déplacer vers la droite, vers sa position d'équilibre initiale. Le déplacement se fait donc de la partie à haute pression, qui voit son volume augmenter, vers la partie à basse pression qui voit son volume chuter. Si l'on se souvient que la grandeur intensive est ici la pression et que la grandeur extensive est ici le volume, cet exemple illustre l'énoncé suivant correspondant à une autre formulation du second principe :

L'énergie s'écoule toujours de la haute intensité vers la basse intensité par un transfert d'extensité.

Dans ce cas: δW = - p.dV

Si l'on met en contact deux objets à potentiels électrostatiques différents, l'énergie ira du plus haut potentiel (grandeur intensive) vers le plus bas par un transfert de charges (grandeur extensive): dE = v.dq .

De même, si l'on met en contact deux sources à températures différentes, la chaleur s'écoulera de la source à haute température vers celle à basse température par transfert d'entropie. L'entropie est donc l'extensité associée à la forme énergétique appelée chaleur: δQ = T.dS .

Second principe et chaos

Boltzmann a étudié le second principe sous son aspect microscopique ce qui a révolutionné la physique, mettant fin aux espoirs de Laplace fondés sur un déterminisme intégral.

Dans la statistique de Maxwell-Boltzmann, on raisonne en effet sur un grand nombre de particules indiscernables, indépendantes et identiques. Dans ce cas, l'entropie d'un macro-état Ω est défini (de façon statistique) par la formule de Boltzmann : S = k_b.ln Ω .

Ω correspond au nombre de micro-états différents observables dans un macro-état donné.

Les cycles de Poincaré

Le célèbre mathématicien Henri Poincaré démontra en 1890 un théorème extrêmement général, dont l'énoncé physique est : « Tout système macroscopique repasse une infinité de fois aussi près que l'on veut de son état initial. » Ce « théorème de récurrence » fut opposé au second principe, car il implique que toute évolution macroscopique est réversible. Pour contrer ce théorème apparemment inattaquable, Boltzmann calcula le temps nécessaire à 100 cm³ de gaz pour revenir à son état initial. Il trouva années !!! Autant dire que, si le problème des cycles de Poincaré subsiste, il n'est pas d'une urgence brûlante (voir dans le même ordre d'idée, l'exemple du jeu de 52 cartes, désordonné dans l'article "entropie").

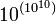
La boîte de Maxwell

Soit une boîte circulaire plate, horizontale, séparée par un diamètre en 2 compartiments égaux, et contenant N palets blancs et N palets noirs, de même rayon r, glissant sans frottements sur ce fond. Ouvrir le diamètre d'une grandeur supérieure à 2r, pour permettre le passage des pions. Secouer, puis immobiliser la boîte : il est assez intuitif que l'état le plus souvent réalisé est celui pour lequel il y aura N/2 palets blancs et N/2 palets noirs dans le compartiment 1 ; ceci avec d'immenses fluctuations, d'autant plus grandes en valeur absolue que la boîte sera grande et que N sera grand : ces fluctuations croissent comme . Mais plus N est grand, plus ces fluctuations seront négligeables devant N et la répartition se rapprochera de N/2 pour chaque couleur de palet dans chaque compartiment. On remarque ici un autre aspect du second principe qui montre que l'évolution spontanée d'un système va toujours vers l'homogénéité.