Diagramme de Minkowski - Définition

Construction du diagramme et règles de transformation des coordonnées

Représentation asymétrique

Règle de projection d'un évènement A sur les axes (x,ct) et (x', ct')

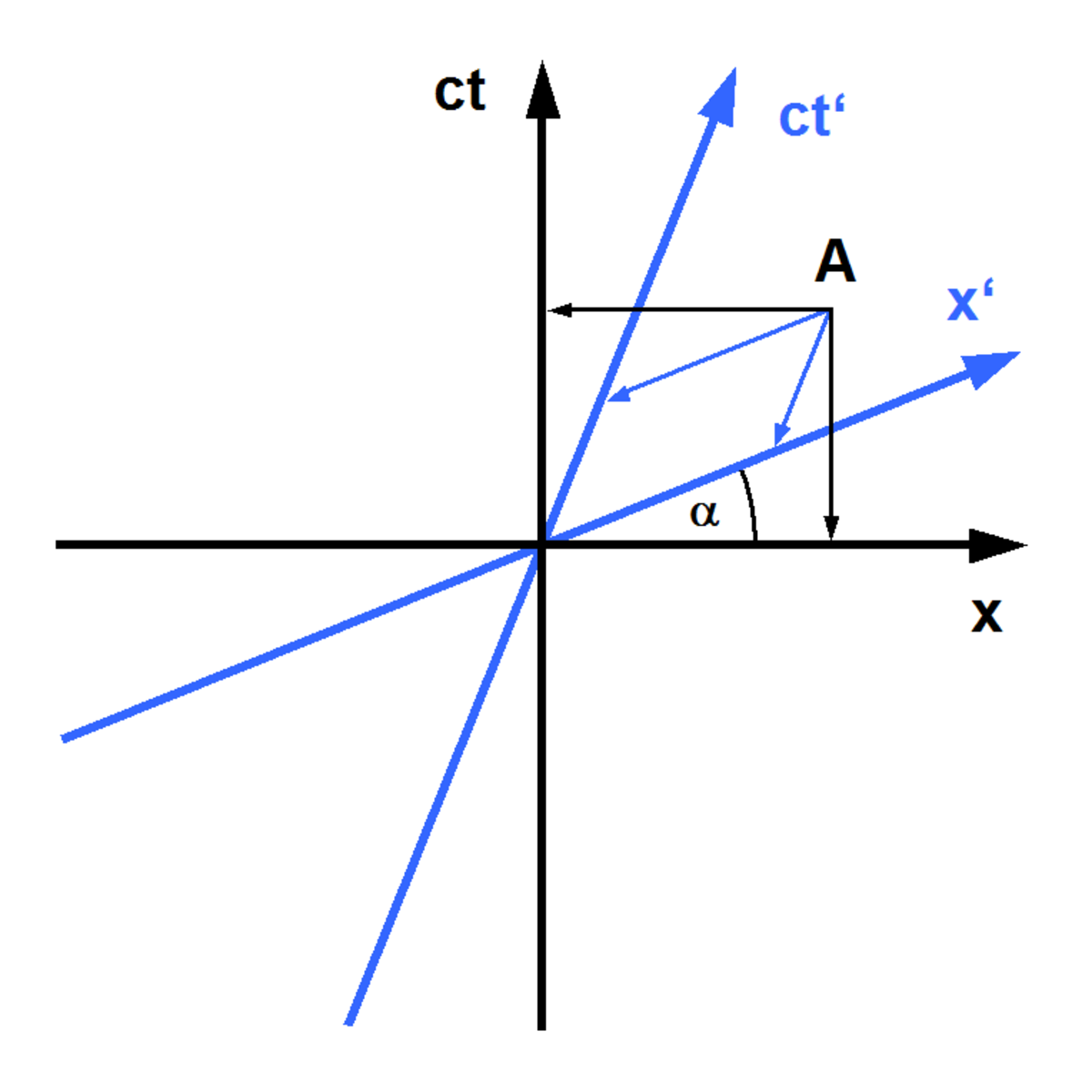
Dans une représentation asymétrique (la plus commune), où un référentiel (x,ct) est considéré au repos et l'autre (x',ct') en mouvement avec une vitesse v (rectiligne et uniforme) par rapport à lui, le diagramme de Minkowski se construit en représentant le premier référentiel avec des axes orthogonaux.

Détermination des axes du second référentiel :

Le second référentiel est représenté avec un axe (O,ct') identifié avec la droite d'équation (ou encore x = β.ct, avec β = v / c) et (O,x') avec la droite symétrique par rapport à la droite d'équation x = ct, c'est-à-dire est d'équation x = (c² / v).t (ou encore x = β ^{− 1}.ct).

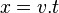
D'un point de vue angulaire, cela signifie que l'axe (O,ct') fait un angle α par rapport à (O,ct) et (O,x') fait le même angle mais de sens opposé par rapport à (O,x), et que l'angle α est tel que .

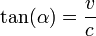
Graduation des axes (O,ct') et (O,x') :

Les transformations de Lorentz nous donnent les relations avec et

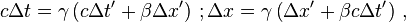
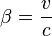
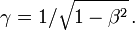
Pour le point de coordonnées (0';1') (donc x' = 0 et ct' = 1), on a : ct = γ > 0 et x = γβ > 0 qui forment un couple de solutions positives de l'équation c²t² − x² = 1.

De même, pour le point (1';0') (donc x' = 1 et ct' = 0), on a : ct = γβ > 0 et x = γ > 0 qui forment un couple de solutions positives de l'équation c²t² − x² = − 1.

En fait, cette détermination de la graduation utilise l'invariance de l'intervalle d'espace-temps par changement de référentiel : .

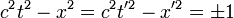
Géométriquement, pour placer les points (0';1') et (1';0'), il suffit de considérer le point commun de coordonnées positives de (O,ct') et de la courbe c²t² − x² = 1, d'une part, et le point commun de coordonnées positives de (O,x') et de la courbe c²t² − x² = − 1, d'autre part.

Détermination des coordonnées d'un point :

Les coordonnées (x,ct) et (x',ct') d'un même évènement A se trouvent par projection sur chaque axe, parallèlement à l'autre axe du référentiel, conformément aux règles usuelles des coordonnées cartésiennes.

Cette représentation est alors apte à décrire un certain nombre de raisonnements qualitatifs et quantitatifs : dilatation des durées, contraction des longueurs, combinaison des vitesses... combinaison de transformation de Lorentz successives (unidimensionnelles).

Représentation symétrique

Représentation symétrique, avec les lignes de simultanétité pour chaque observateur.

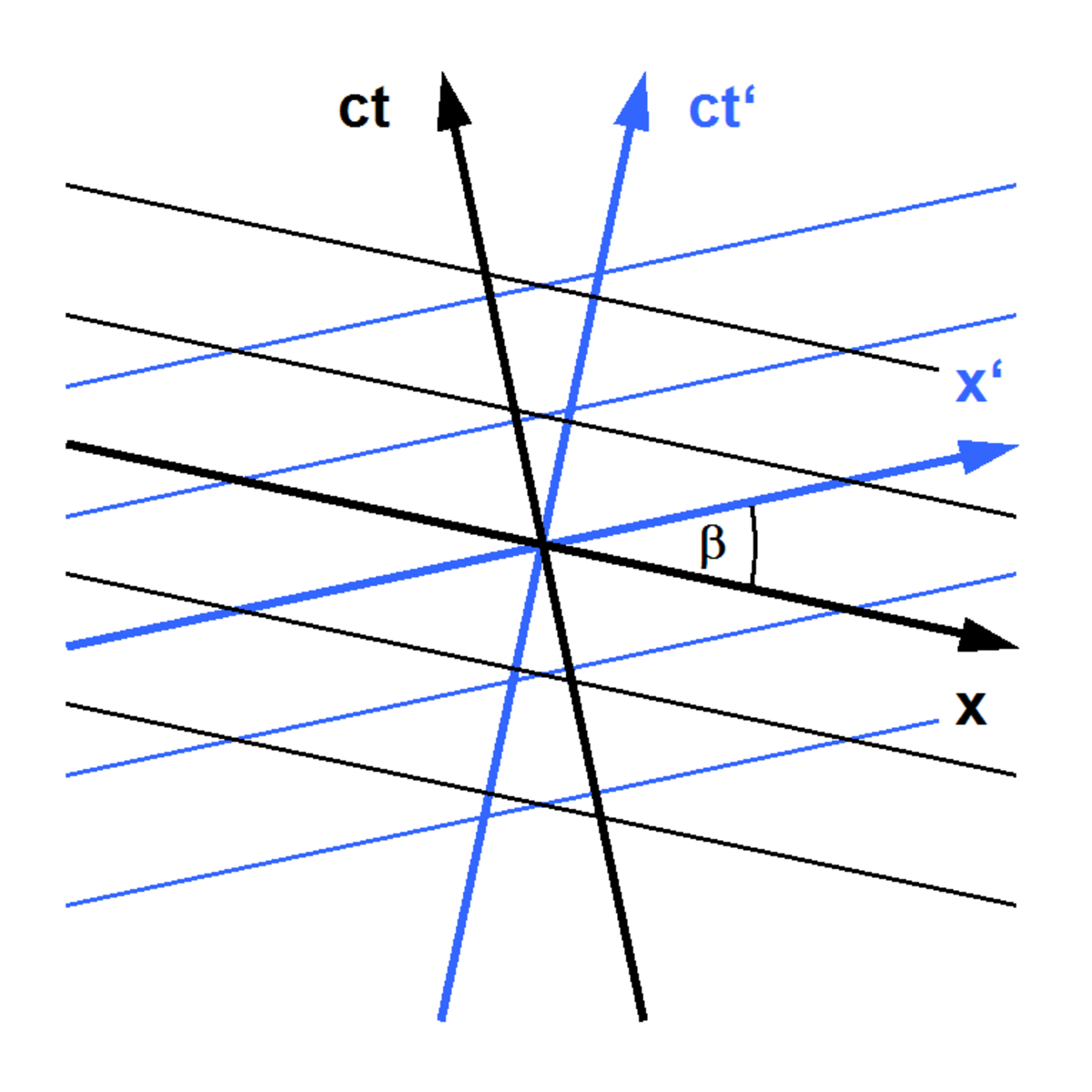
Il existe une représentation symétrique du diagramme de Minkowski (appelée également diagramme de Loedel d'après le physicien Enrique Loedel Palumbo qui a introduit le premier cette représentation symétrique) où aucun référentiel n'est privilégié. Les deux systèmes d'axes sont représentés symétriquement par rapport aux directions orthogonales, et sont séparés par un angle β tel que :

.

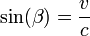
Contrairement à la représentation asymétrique, l'échelle et la graduation des axes des deux référentiels est la même, ce qui facilite l'interprétation des figures. Cette représentation apparaît plus proche de l'esprit de la relativité où aucun référentiel n'est privilégié.

Exemples d'application du diagramme de Minkowski

Dilatation temporelle

Dilatation temporelle : les deux observateurs considèrent que le temps passe plus lentement dans l'autre référentiel

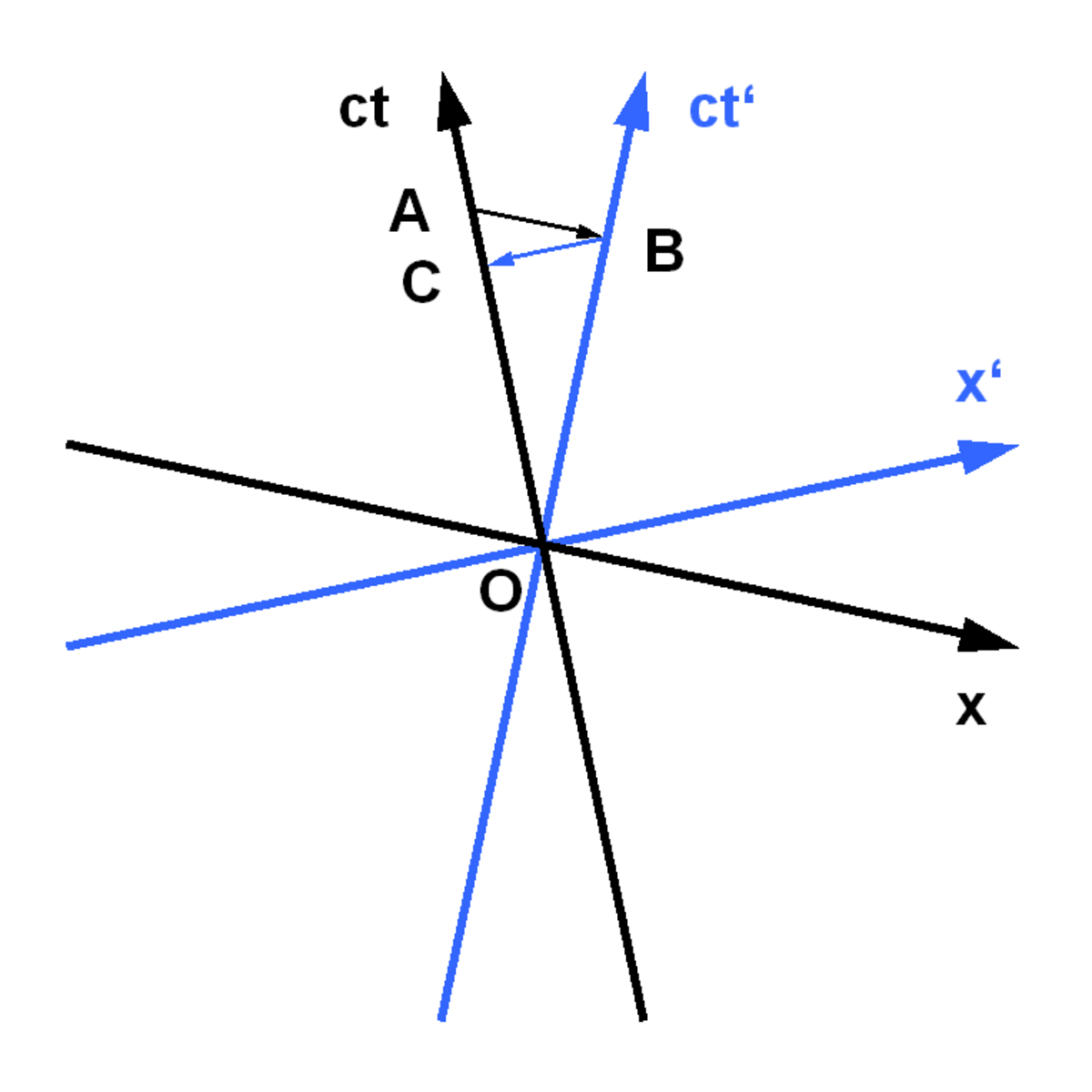
Selon la théorie de la relativité restreinte, une horloge animée d'une certaine vitesse par rapport à un référentiel qualifié de fixe sera observée comme battant le temps à un rythme plus lent que celui des horloges de ce référentiel.

Cette constatation est réciproque, c'est-à-dire que l'horloge dans le repère "fixe" sera également observée comme plus lente que celles du référentiel en mouvement, à partir de ce dernier référentiel, ce qui semble à première vue paradoxal.

Ceci peut être visualisé avec un diagramme de Minkowski. Pour un observateur en A (voir schéma ci-contre), le temps "simultané" de l'autre référentiel est le temps en B qui est inférieur à A. L'observateur en A peut donc logiquement conclure que le temps se passe plus lentement dans l'autre référentiel. Réciproquement, pour un observateur en B, le temps "simultané" de l'autre référentiel est en C, qui est inférieur à B, et observe également un ralentissement du temps dans l'autre référentiel.

La vitesse de la lumière comme vitesse limite

Emission d'un message vers le passé, à une vitesse supraluminique, de O à B via A.

Le diagramme de Minkowski permet d'illustrer les contradictions et paradoxes qui interviennent à partir du moment où on postule qu'une information peut se propager à une vitesse supérieure à celle de la lumière.

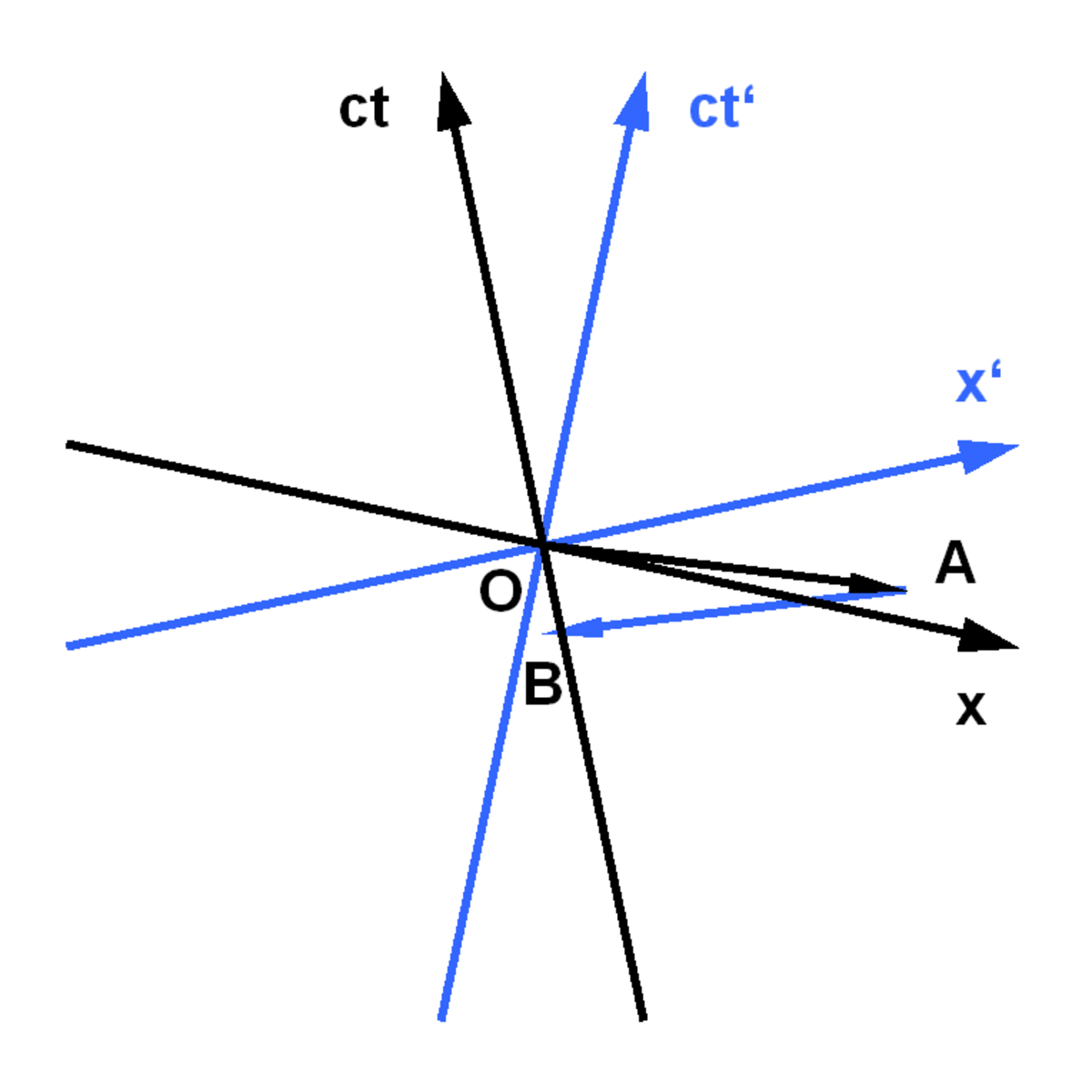
Si un observateur en O est en mesure d'émettre un message vers A à une vitesse supraluminique, alors A peut réfléchir- supraluminiquement également - le message vers la position de O. Le diagramme de Minkowski montre que le message arrive alors dans le passé de l'observateur O (évènement B), avant que celui-ci ne l'ait envoyé..

De plus, pour l'observateur dans le référentiel (x,ct), l'évènement B a lieu avant l'évènement A, alors que l'ordre temporel apparait inverse pour un observateur dans le référentiel (x',ct'). Pour le premier observateur, B est la cause de A, alors que pour le second A est la cause de B. Ceci est une violation du principe de causalité selon lequel la cause précède toujours l'effet.

Ces considérations montrent que la limite de la vitesse de la lumière est une conséquence des propriétés de l'espace-temps et de la notion de causalité, et non une conséquence liées aux propriétés physiques des objets eux-mêmes, comme des limites technologiques par exemple.