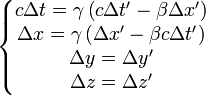Contraction des longueurs - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En relativité restreinte, la contraction des longueurs désigne la loi suivant laquelle la mesure de la longueur d'un objet en mouvement est diminuée par rapport à la mesure faite dans le référentiel où l'objet est immobile, du fait, notamment, de la relativité de la simultanéité d'un référentiel à l'autre. Toutefois, seule la mesure de la longueur parallèle à la vitesse est contractée, les mesures perpendiculaires à la vitesse ne changent pas d'un référentiel à l'autre.
En relativité générale, une contraction des longueurs est aussi prédite. Dans ce cadre, sa cause en est soit la même qu'en relativité restreinte, soit la gravitation ou une accélération.
En relativité restreinte
Mesure de la longueur d'un objet
Dans un référentiel quelconque de l'espace-temps, mesurer un objet c'est avoir deux détecteurs, immobiles et espacés d'une distance connue, qui sont simultanément en contact avec les extrémités de cet objet. Dans ce cas, la longueur de l'objet est la distance entre les deux détecteurs.
En considérant deux référentiels

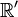
L'invariance de l'intervalle d'espace-temps s'écrit :
-
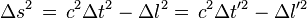
- où
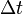
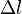

- Deux détecteurs étant donnés, les deux événements considérés sont le contact de chacun avec une extrémité.
Si la mesure est faite dans le référentiel
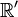
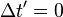
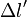
Vu de

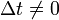
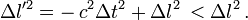
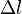

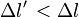
Immobilité ou pas
On suppose que l'objet est immobile dans le référentiel

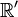
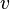
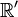


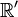
Dans le référentiel

Ainsi dans
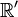
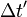
- Dans
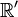
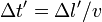
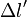
- Dans

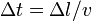
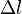
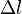
Par l'invariance de l'intervalle d'espace-temps, on a
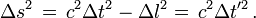
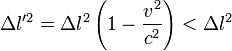
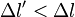
Mesurer un mètre avec un mètre
Supposons que dans chaque référentiel on dispose d'un mètre (immobile) avec lequel on mesure la longueur du mètre immobile dans l'autre référentiel et orienté dans la direction de la vitesse relative.
Suivant le raisonnement du deuxième paragraphe, dans chaque référentiel on doit voir le mètre de l'autre référentiel plus petit que celui qui est immobile. Est-ce un paradoxe ? Non.
- Prenons le cas où la mesure est faite depuis

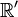

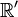

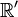

Cas des longueurs perpendiculaires à la vitesse
Les longueurs perpendiculaires à la direction du mouvement ont la même mesure dans les deux référentiels.
- Pour s'en convaincre, il suffit d'imaginer une porte coulissante, entre des rails supérieurs et inférieurs, immobile dans un référentiel et que l'on accélère dans ce même référentiel (les rails du coulissement sont très très longs) : les rails supérieurs et inférieur sont immobiles et sont toujours à la même distance, et la porte, animée d'une vitesse peut-être très grande, ne sort pas de ses rails du simple fait qu'elle les suit. La hauteur de la porte, longueur perpendiculaire à la vitesse, reste égale à la distance entre les rails supérieurs et inférieurs, donc ne diminue pas dans le référentiel où on la voit passer, par rapport au moment où elle était immobile.
Avec les transformations de Lorentz
Les transformations de Lorentz sont, en supposant la vitesse parallèle à l'axe (ox) et en posant
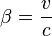
 :
:
Pour la mesure faite dans le référentiel
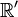
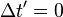
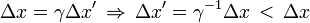
On montre aussi la non simultanéité de la détermination des extrémités vue depuis l'autre référentiel :
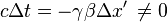
Contraction des volumes
La translation d'un volume par rapport à un référentiel inertiel implique que la dimension de ce volume ayant la même direction que le mouvement est contractée d'un facteur γ − 1, si la mesure est faite dans le dit référentiel et par rapport à une mesure faite sur le volume au repos. Les mesures des dimensions perpendiculaires au mouvement ne sont pas contractées. Par produit entre ces différentes mesures, cela implique que les volumes sont aussi contractées du même facteur γ − 1.