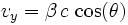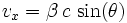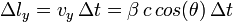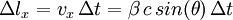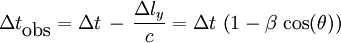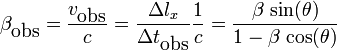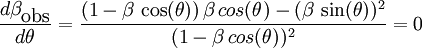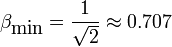Vitesse supraluminique - Définition

Introduction

Une vitesse supraluminique (superluminal en anglais) désigne une vitesse supérieure à la vitesse de la lumière. Sous ce terme, on désigne aussi bien des phénomènes optiques tels que ceux rencontrés dans les quasars et les microquasars (jets semblant se déplacer vers l'observateurs à des vitesses ultraluminiques) et qui ne résultent que de la finitude de la vitesse de la lumière, qu'une collection d'effets de nature quantique. Vitesse supraluminique peut aussi se traduire en anglais par Faster-than-Light (FTL). Mais dans ce cas, on parle surtout de voyage et de transmission d'information plus rapide que la lumière, et ce terme relève alors plutôt du domaine de la science-fiction.

La théorie de la relativité stipule que, dans le vide, les luxons, particules de masse au repos nulle (comme les photons par exemple), se déplacent à la vitesse c, naturellement appelée vitesse de la lumière, et que cette vitesse est une limite asymptotique ne pouvant pas être atteinte par les bradyons, corps de masse au repos non-nulle, ainsi que pour les tachyons, corps hypothétiques de masse au repos imaginaire. Dans le cadre de cette même théorie, on déduit que toute particule ayant une masse au repos non-nulle aurait besoin d'acquérir une quantité d'énergie infinie (ce qui est impossible) pour atteindre cette vitesse (d'une manière similaire, tout tachyon aurait à acquérir une énergie infinie pour ralentir jusqu'à atteindre cette vitesse).
Les effets quantiques mentionnés ne contredisent pas cette limite, mais restent à ce jour soit extrêmement hypothétiques, soit la contournent conceptuellement en explorant les limites de nos connaissances sur les interactions entre les particules et la matière. Dans ce cadre, ils font l'objet de nombreuses expérimentations. Enfin, il existe d'autres phénomènes supraluminiques qui sont des objets définis par la pensée et dont la présentation succincte permet simplement de mettre en exergue l'impossibilité pour l'information ou l'énergie de se déplacer plus vite que c.

Dès 1907, Arnold Sommerfeld relevait la possibilité de vitesses de groupes supérieures à c dans la théorie maxwellienne de l'électromagnétisme. Il engagea le jeune Léon Brillouin sur cette piste. Il s'avéra rapidement que le concept de 'vitesse de la lumière' était justiciable non pas d'une, mais d'une demi-douzaine de définitions distinctes : vitesses de groupe et de phase, de signal (la vitesse intuitive des mécaniciens), de front, de sommet, de transport de l'énergie, de transport de l'information...

La théorie de la relativité ne limitant a priori que les deux dernières (transports d'énergie et d'information), et celles qui y sont indirectement reliées (comme celle de front, dans sa définition stricte), les autres grandeurs, et en particulier les vitesses de groupe et de signal, peuvent dans certains cas prendre des valeurs quelconques, entre zéro et l'infini (ou des valeurs négatives). Des vitesses de signal supraluminiques peuvent en particulier être observées dans des expériences d'optique non linéaire.

En astrophysique

Présentation

En astrophysique, des vitesses supraluminiques apparentes sont parfois observées dans les jets des quasars et des microquasars. Ce phénomène n'est que le résultat d'un effet de projection et de la finitude de la vitesse de la lumière. On trouve dans ces deux classes d'objets un trou noir autour duquel se trouve un disque d'accrétion. Le disque est traversé par un champ magnétique qui permet de propulser des jets, selon un axe perpendiculaire au disque et centré sur le trou noir.

Il n'est pas encore clairement expliqué comment un jet produit par un disque d'accrétion peut atteindre une vitesse suffisamment grande pour sembler supraluminique à un observateur lointain. En effet, même si cet effet est géométrique comme décrit ci-dessous, il faut quand même que le jet atteigne une vitesse minimale pour apparaître comme supraluminique. Un modèle prometteur, développé au LAOG en France, propose qu'à l'intérieur d'un jet classique non-relativiste (c'est-à-dire n'atteignant pas des vitesses semblables à celle de la lumière) se crée sous certaines conditions des paires électrons-positrons. Le jet classique, auto-collimaté par le champ magnétique, permettrait de créer un jet de ces paires atteignant alors des vitesses ultra-relativistes (très proches de c).

Dans notre galaxie, la Voie lactée, le premier objet montrant de tels jets fut découvert en 1994 et s'appelle GRS 1915+105, et où la vitesse des jets semble être de 1,3 fois celle de la lumière. Ces jets supraluminiques sont observés généralement dans les ondes radio avec des instruments tels que le VLA ou le VLBA. Des jets supraluminiques sont aussi observés dans le microquasar XTE J1550-564.

Démonstration

Les vitesses supraluminiques observées en astrophysique résultent d'un phénomène bien compris et en aucun cas des particules de masse non-nulle ne se déplacent réellement à des vitesses supérieures à c. Il n'y a donc pas violation du postulat de la relativité restreinte.

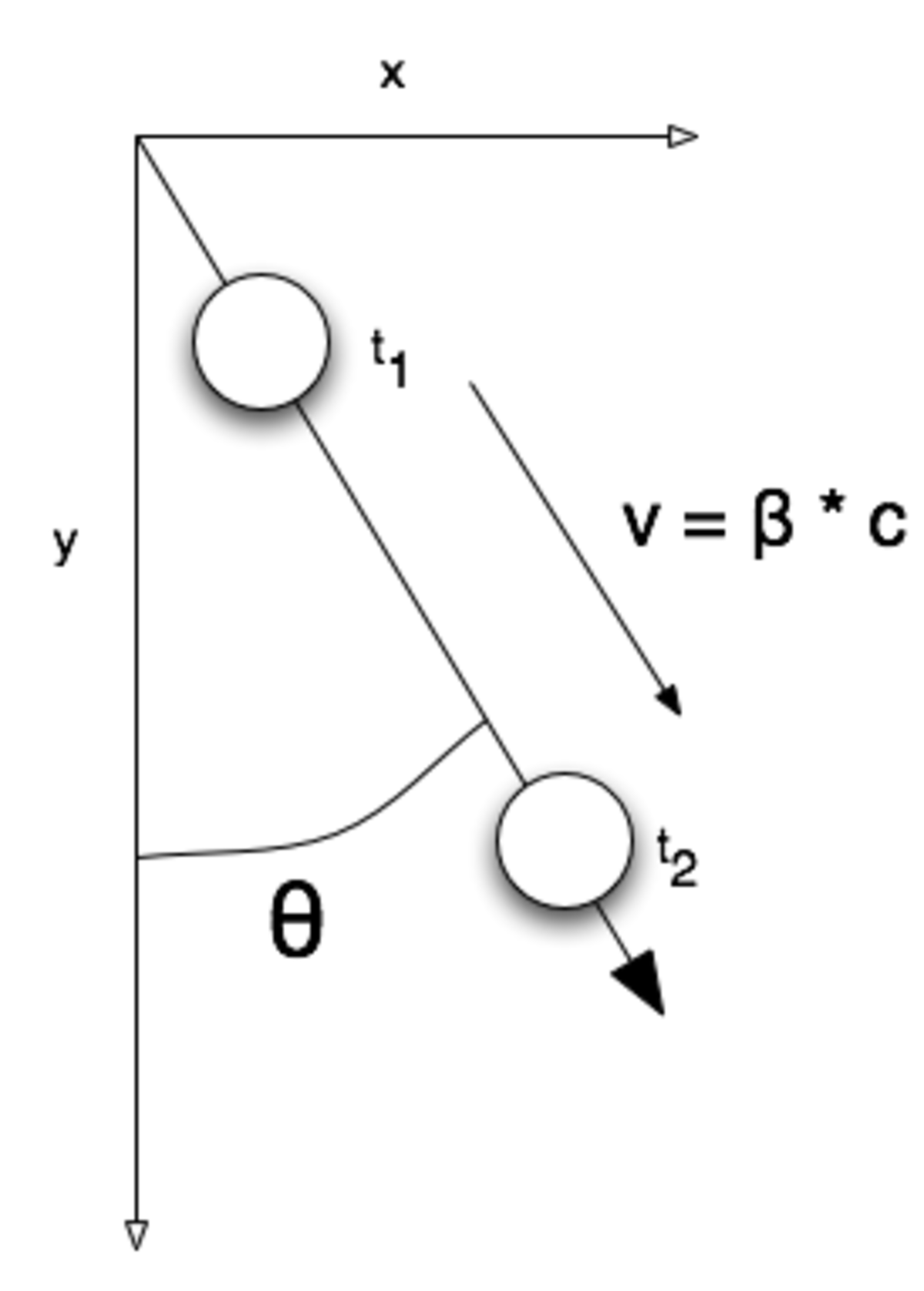
Sur la figure est représenté par un cercle un objet matériel (paquet de gaz, de particules), projeté par le (micro)quasar émettant de la lumière et se déplaçant de haut en bas selon la flèche inclinée, avec une vitesse v. On se place dans le référentiel de l'observateur que nous sommes (ex : un astronome observant un microquasar...). L'observateur est situé en bas de la figure, très loin sur l'axe «y». On observe l'objet dans sa position du haut à un temps t₁, et en bas à un temps t₂, (avec t₁ < t₂).

Schema décrivant le déplacement d'un objet (le rond) le long d'une direction (la flèche). L'observateur se trouve dans la direction de l'axe «y», en bas.

On définit par commodité: , où c est la vitesse de la lumière. Naturellement, . Pour toute particule ayant une masse non-nulle, . Pour la lumière, β = 1.

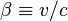
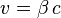
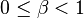
Puisqu'il existe un angle θ entre l'axe «y» et la direction de l'objet dans l'espace, la vitesse de l'objet en mouvement projetée sur les axes «x» et «y» s'écrivent respectivement, par simple trigonométrie:

Si l'on définit l'intervalle de temps entre t₁ et t₂ comme Δt = t₂ − t₁, les intervalles de longueur projetés sur les axes «x» (Δl_x) et «y» (Δl_y) du déplacement de l'objet s'obtiennent comme:

Entre le temps t₁ et le temps t₂, l'objet s'est déplacé selon l'axe «y» d'une longueur Δl_y. Mais l'observateur se trouvant à très grande distance de l'objet, il ne peut pas percevoir le mouvement le long de l'axe «y», et l'objet ne semble s'être déplacé que transversalement. En apparence donc, la lumière émise au temps t₁ et celle au temps t₂ a été émise à la même distance de l'observateur. Donc en apparence, le temps observé est plus court que le temps réel, puisque le temps mis par la lumière pour parcourir Δl_y n'est pas perçu.

On pourrait dire à l'inverse que l'intervalle de temps effectivement observé est plus court que l'intervalle de temps vrai, puisque la lumière a économisé la distance Δl_y entre les deux observations, distance qui est non négligeable lorsque la vitesse réelle est comparable à celle de la lumière. Pour des vitesses habituelles à l'échelle humaine qui sont très faibles devant la vitesse de la lumière, ce temps est minuscule et parfaitement indétectable. Mais dans le cas où l'objet matériel se déplace avec une vitesse comparable à celle de la lumière ce temps n'est pas négligeable. Ainsi :

Pour des vitesses à l'échelle humaine, β est extrêmement petit, et le terme tend donc vers 0. Dans ce cas, les intervalles de temps observés et réels sont égaux. De même, pour un angle , le cosinus est nul, la projection le long de l'axe «y» est nulle, et l'effet aussi. Si , on ne voit pas l'objet se déplacer transversalement. Il existe donc un angle intermédiaire, pour lequel cet effet est maximal. Si β est assez grand alors la vitesse apparente maximale est plus grande que celle de la lumière.

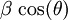
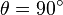
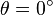
En effet, la vitesse observée (en fait calculée à partir des observations) transversalement, le long de l'axe «x», ou mieux, en divisant par c :

Courbes de la vitesse observée β_obs en fonction de θ, pour différentes valeurs de la vitesse réelle du mouvement, β qui, elle, reste toujours inférieure à la vitesse de la lumière.

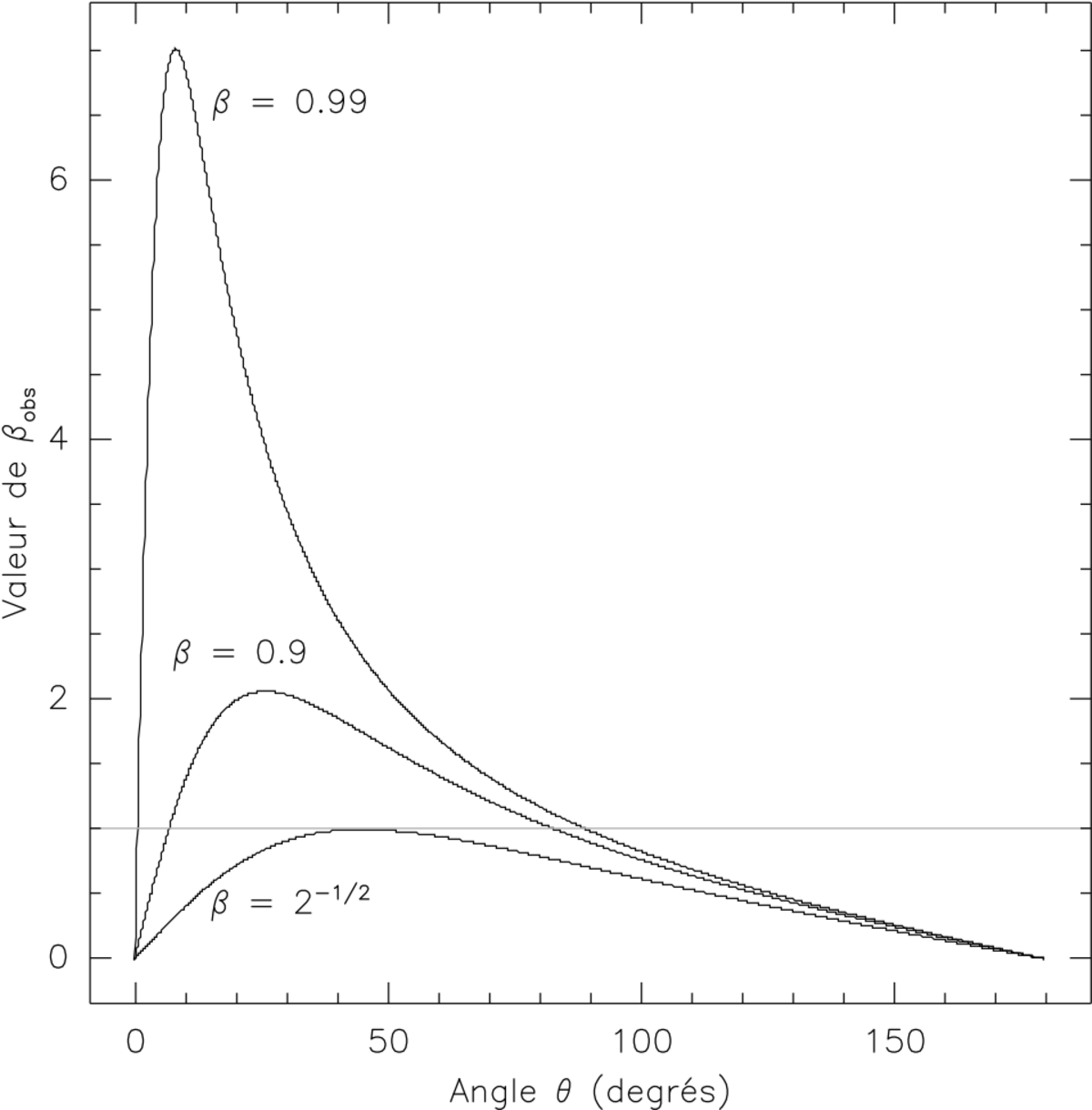
Cette fonction de θ est illustrée sur la figure ci-contre, et peut dépasser 1 ! Donc la vitesse observée peut dépasser la valeur de la vitesse de la lumière, même si la vitesse réelle est plus petite (ou en d'autres termes β_obs > 1. même si β < 1.).

On obtient la position du maximum de la courbe en annulant sa dérivée :

Donc le terme supérieur doit être nul, ce qui implique que le maximum de la courbe s'obtient lorsque β = cos(θ).

Il existe une valeur minimum de β en dessous de laquelle la vitesse observée ne peut jamais être supérieure à la vitesse de la lumière. Inversement, si β est plus grand que cette valeur, il existe toujours au moins un angle pour lequel la vitesse observée est plus grande que la vitesse de la lumière (c'est-à-dire β_obs > 1). En remplaçant β par cos(θ) dans l'expression de β_obs, et en égalant à 1 pour obtenir le maximum de la courbe exactement à la vitesse de la lumière, on obtient que dans ce cas particulier : β = cos(θ) = sin(θ), et que :

Ce qui correspond à environ 212 000 km/s.