Distance de Hamming - Définition
La liste des auteurs de cet article est disponible ici.
Définition et exemples
Définitions
- Soit A un alphabet et F l'ensemble des suites de longueur n à valeur dans A. La distance de Hamming entre deux éléments a et b de F est le nombre d'éléments de l'ensemble des images de a qui diffèrent de celle de b.
Formellement, si d(.,.) désigne la distance de Hamming :
![\forall a,b \in F \quad a = (a_i)_{i\in [0, n-1]} \; et \; b = (b_i)_{i\in [0, n-1]} \quad d(a,b) = \#\{ i : a_i\neq b_i \}](https://static.techno-science.net/illustration/Definitions/autres/7/71699525f9403e3b1588348a97f277d7_a10d9819dd394a9a9bd35c66f9487ed7.png)
La notation #E désigne le cardinal de l'ensemble E.
Un cas important dans la pratique est celui des symboles binaires. Autrement dit A= {0,1}, On peut alors écrire, si ⊕ désigne le ou exclusif.
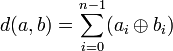
Dans le cas, fréquent, où l'alphabet est un corps fini, F possède une structure d'espace vectoriel de dimension n. La distance dérive alors d'une pseudo-norme :
- Soit K est un corps fini et F l'ensemble des suites de longueur n à valeur dans K. Le poids de Hamming p(a) d'un élément a de F est le cardinal de l'ensemble des images de a non nulles.
L'alphabet est souvent F2 le corps à deux éléments {0,1}. Le poids de Hamming est une pseudo-norme car :
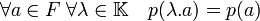
Néanmoins, si l'alphabet est un corps fini, alors la distance dérive du poids de Hamming, en effet:
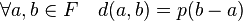
Exemples
Considérons les suites binaires suivantes :
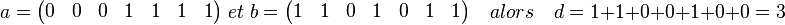
La distance entre a et b est égale à 3 car 3 bits diffèrent.
- La distance de Hamming entre 1011101 et 1001001 est 2.
- La distance de Hamming entre 2143896 et 2233796 est 3.
- La distance de Hamming entre "ramer" et "cases" est 3.
Cas binaire
Un cas important est celui ou l'alphabet est le corps à deux éléments {0,1}. Une lettre est alors appelée bit. Il est largement utilisé en informatique et en télécommunication.
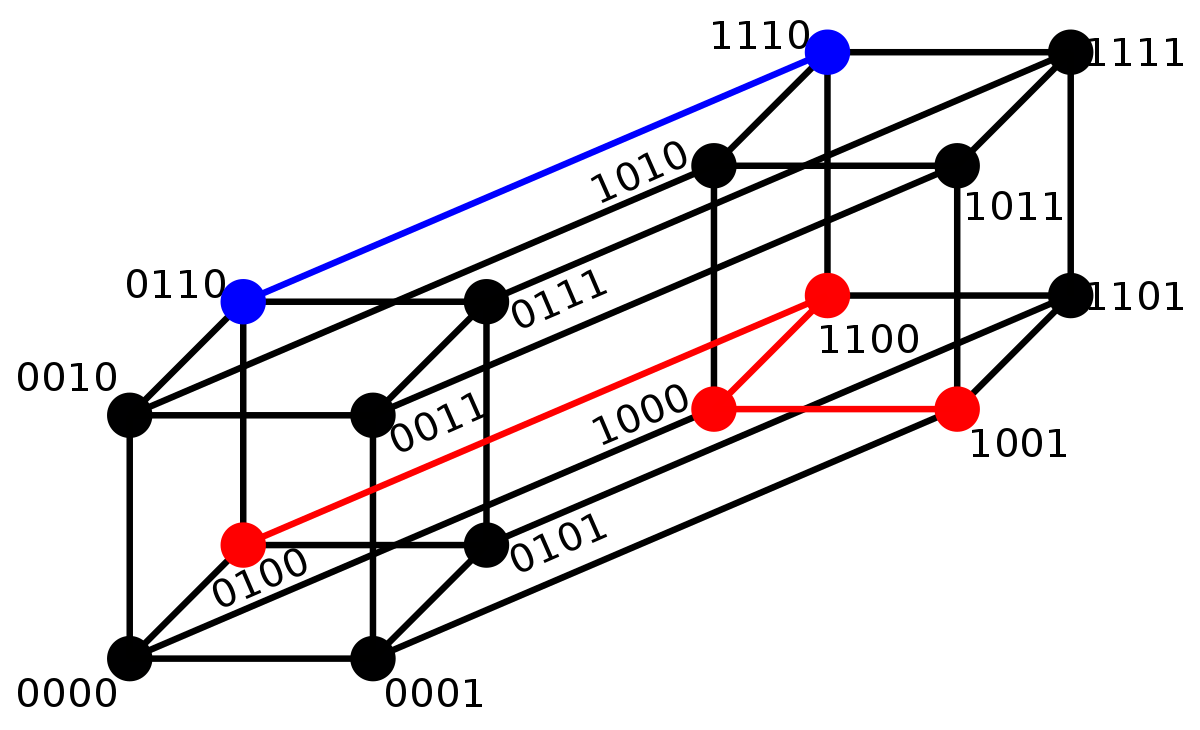
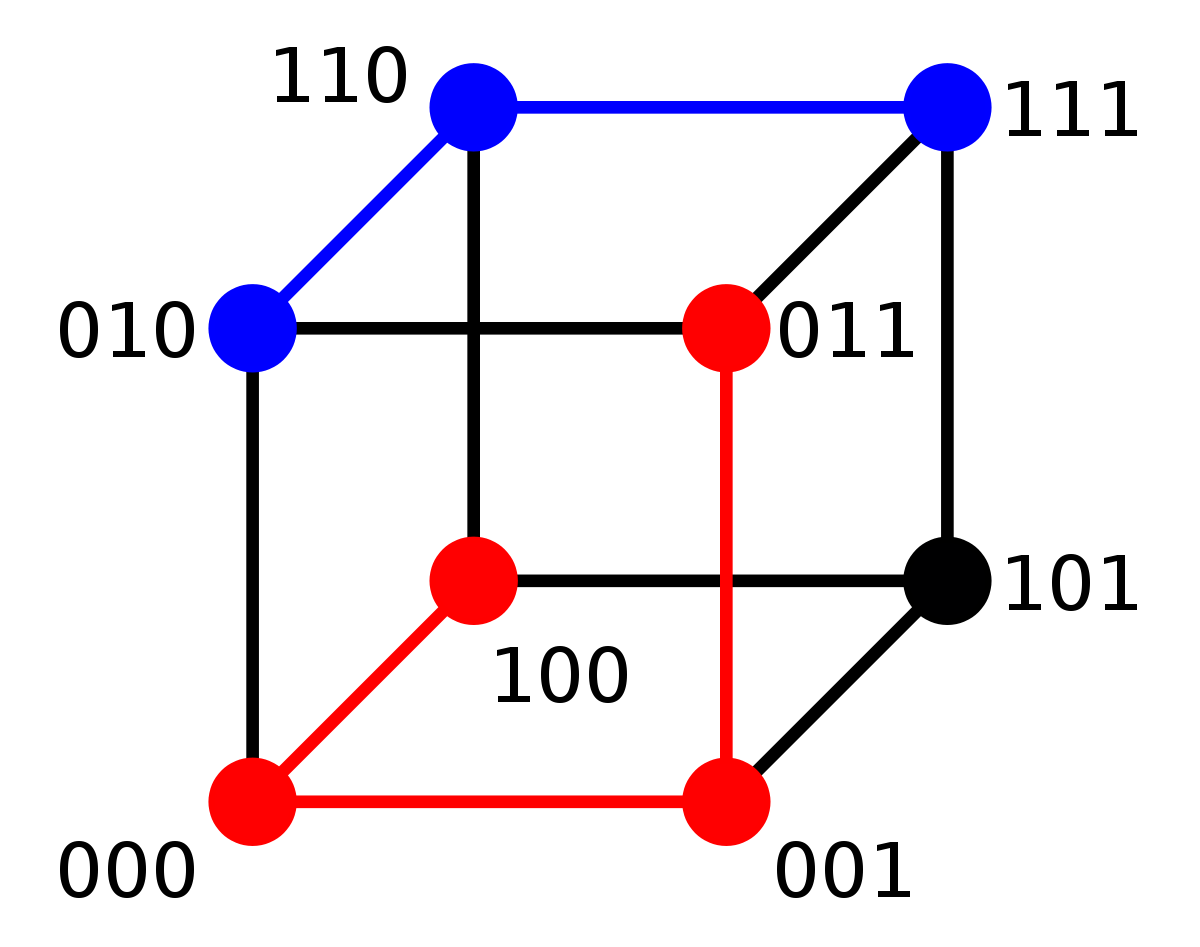
Il est possible d'illustrer graphiquement le code et les distances entre les différents mots.
Le cas ou un mot comporte trois lettres est illustré sur la figure de gauche. La distance entre 010 et 111 est égale à deux car il est nécessaire de parcourir deux segments pour joindre les deux points. La distance pour joindre les points 100 et 011 est égale à trois.
La figure de droite illustre un hypercube binaire de dimension quatre. La distance entre 0110 et 1110 est égale à un, alors que la distance entre 0100 et 1001 est égal à trois.
Le poids de Hamming d'un élément a correspond à la distance entre le mot zéro n'ayant que des coordonnées nulles et a.
Applications
Somme de contrôle
| Données sur 7 bits | avec bit de parité |
|---|---|
| 0000000 | 00000000 |
| 1010001 | 11010001 |
| 1101001 | 01101001 |
| 1111111 | 11111111 |
La somme de contrôle est un exemple simple d'utilisation de la distance de Hamming. La distance minimale entre deux mots du code est égale à deux. En conséquence, si une unique erreur se produit elle est détectée. En revanche, elle n'est pas corrigeable sans retransmission. En effet, il existe a priori plusieurs mots de code à distance de un du message erroné.
L'exemple le plus simple est celui du bit de parité. Il correspond à une somme de contrôle dans le cas où le corps est binaire, c'est-à-dire qu'il contient deux éléments zéro et un.
Supposons que l'objectif soit la transmission de sept bits. Un bit de parité est défini comme étant égal à zéro si la somme des autres bits est paire et à un dans le cas contraire. Les huit bits transmis sont d'abord le bit de parité puis les sept bits du message. Il correspond au bit de parité pair, c'est-à-dire la deuxième colonne du tableau de droite. Les messages envoyés sur huit bits ont toujours la parité zéro, ainsi si une erreur se produit, un zéro devient un un, ou l'inverse; le récepteur sait qu'une altération a eu lieu. En effet la somme des bits devient impaire ce qui n'est pas possible sans erreur de transmission.
Code de Hamming
Le code de Hamming est un exemple un peu plus complexe que le précédent. La distance minimale entre deux mots du code est égale à trois. Si une unique altération se produit, alors le message reçu est à une distance de un d'un unique point du code. Il est ainsi possible de corriger automatiquement une erreur, si l'on sait que l'erreur est unique.
Code linéaire
Les codes linéaires forment une famille contenant les deux exemples précédents. L'alphabet est un corps fini, les ensembles E et F sont des espaces vectoriels et l'application φ est linéaire. La distance de Hamming dérive de la pseudo-norme : le poids de Hamming. Ce contexte est très généralement celui qu'utilise l'industrie.
Code cyclique
Cette famille de codes correspond à un cas particulier de code linéaire. Les structures E et F sont enrichies d'une structure d'anneau leur conférant le statut d'algèbre. Cette structure, se fondant sur la théorie polynômes sur les extensions de corps finis permet de construire des distances minimales aussi élevées qu'on le souhaite.
De nombreux codes sont construits sur cette théorie. Le code de Hamming apparaît comme un cas particulier de ceux là. On peut citer aussi les codes BCH ou les codes de Reed-Solomon utilisés par exemple pour les disques compacts.