Droite projective - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Coordonnées homogènes - Exemples

Introduction

En géométrie, une droite projective est un espace projectif de dimension 1.

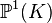
En première approche (en oubliant sa structure géométrique), la droite projective sur un corps K, notée $\mathbb P ^1(K)$ , peut être définie comme l'ensemble des droites vectorielles du plan vectoriel K². Cet ensemble s'identifie à la droite K à laquelle on ajoute un point à l'infini.

La notion de droite projective se généralise en remplaçant le corps K par un anneau associatif.

Coordonnées homogènes

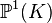
En coordonnées homogènes, un point sur la droite projective $\mathbb P ^1(K)$ est représenté par une paire de la forme :

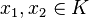
où $x_1, x_2 \in K\,$ ne sont pas tous deux nuls.

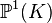
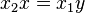
Ce point de $\mathbb P ^1(K)$ correspond à la droite de K² d'équation $x_2x=x_1y\,$ .

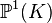
Deux telles paires représentent donc le même point de $\mathbb P ^1(K)$ si elles ne diffèrent que par un facteur non-nul λ :

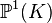
La droite K s'identifie au sous-ensemble de $\mathbb P ^1(K)$ donné par :

(l'élément a de K correspond à la droite de K² d'équation x=ay).

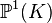
Ce sous-ensemble couvre tous les points de $\mathbb P ^1(K)$ , excepté le point à l'infini

(correspondant à la droite de K² d'équation y=0).

Exemples

Nombres réels

Si K est le corps R des nombres réels, alors la droite projective réelle est obtenue en intersectant les droites vectorielles de R² avec le cercle unité et en identifiant chaque point de ce cercle au point diamétralement opposé (puisqu'il correspond à la même droite). En termes de théorie des groupes, ceci équivaut à prendre le groupe quotient du cercle par le sous-groupe {1,-1}.

La topologie de cet espace quotient est celle d'un cercle. On peut en effet le concevoir en imaginant les +∞ et -∞ des nombres réels collés ensemble pour ne former qu'un seul point à l'infini, ∞, dit point à l'infini dans la direction de la droite réelle.

La droite projective réelle diffère donc de la droite réelle achevée, où une distinction est faite entre +∞ et -∞.

Nombres complexes

Si le corps K est l'ensemble des nombres complexes, on obtient de même la droite projective complexe comme espace topologique quotient, homéomorphe à la sphère usuelle. Elle est aussi connue sous le nom de sphère de Riemann ou sphère de Gauss. Elle s'identifie au plan complexe C auquel on ajoute un point à l'infini.

C'est l'exemple le plus simple de surface de Riemann compacte. Ceci explique qu'on rencontre souvent la droite projective en analyse complexe, en géométrie algébrique et en théorie des variétés complexes.

Corps finis

Wikimedia Commons propose des documents multimédia libres sur Droite projective sur un corps fini.

Si K est le corps corps fini à q éléments, alors la droite projective est constituée de q+1 points. En effet, on peut décrire toutes les droites de K², sauf une, par une équation de la forme x = ay où $a \in K$ . La droite restante est celle d'équation y=0.

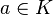
Articles de géométrie projective ou voisins à consulter.

Hexagramme de Pascal • Axiomes de plans projectifs • Théorème de Pappus • Théorème de Desargues • Dualité • Axiomes de plans projectifs/Suite des axiomes • Axiomes de plans projectifs/homogènes • Axiomes de plans projectifs/barycentriques • Plan affine • Théorème d'Hessenberg • Traité projectif des coniques • Traité projectif des coniques/Dans un plan pappusien • Conique • Octonions • Relation d'équivalence • Structure de corps • Construction d'un cercle point par point • Construction d'une parabole tangente par tangente • Plan de Fano • Portail:Géométrie • Géométrie analytique • Géométrie synthétique • Géométrie • Géométrie projective • Géométrie non euclidienne • Division harmonique • Rapport anharmonique • Application projective • Fonction homographique • Perspective • Perspective conique • Infini • Droite (mathématiques)

- Introduction - Coordonnées homogènes - Exemples