Entier de Gauss - Définition

Définition

Formellement, l'ensemble des entiers de Gauss Z[i] est l'anneau des entiers algébriques du corps des rationnels de Gauss, c'est-à-dire l'ensemble des rationnels de Gauss dont le polynôme irréductible normalisé est à coefficients entiers.

Il correspond aux nombres complexes qui peuvent être décrits de la façon suivante :

Les deux définitions sont équivalentes.

L'objectif est de montrer que l'ensemble des entiers de Gauss, c’est-à-dire les rationnels de Gauss ayant un polynôme minimal unitaire à coefficients entiers, est celui des nombres de la forme a + i.b où a et b sont des entiers.

• Si a et b sont entiers alors a + i.b est un entier de Gauss.

En effet, a + i.b est racine du polynôme unitaire à coefficients entiers X² - 2a.X + a² + b²

• Réciproquement si e = a + i.b est un entier de Gauss alors a et b sont des entiers.

Soit P[X] le polynôme minimal de e:

Comme les coefficients du polynôme sont réels, les deux racines sont conjugées et l'on obtient les deux égalités : 2.a = -p et a² + b² = q. Ces égalités montrent qu'il existe deux nombres entiers α et β tel que α = 2.a et aussi β = 2.b car le carré de 2.b est un entier. La deuxième égalité devient :

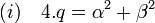
Supposons que α soit impair, alors pour que le deuxième membre de l'égalité (i) soit paire, il est nécessaire que β soit aussi impair. Il existe alors deux entiers α' et β' tels que α = 2.α' + 1 et β = 2.β' + 1. L'égalité (i) devient :

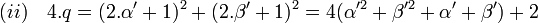
Le deuxième terme de l'équation (ii) est congru à 2 modulo 4 alors que le premier est congru à zéro. En conclusion α ne peut être impair.

Le fait que α soit pair implique que β est aussi pair, en conséquence a et b sont entiers.

 

Arithmétique

La division euclidienne possède des propriétés fortes. Elle permet de construire une arithmétique complète. On parle alors d'anneau euclidien. Cette arithmétique est semblable à celle des entiers.

Anneau principal

Un anneau principal est un anneau dont tous les idéaux sont principaux. L'anneau des entiers de Gauss est principal. Cette propriété est vraie pour tout anneau euclidien.

Pour s'en rendre compte il suffit de considérer un idéal I quelconque et un élément x différent de 0, de plus petite norme dans I. Si y est un élément quelconque de l'idéal, la division de y par x montre que le reste, élément de l'idéal possède une norme plus petite que x, donc est nul.

Identité de Bézout

Comme dans tout anneau euclidien, l'identité de Bézout se généralise aux entiers de Gauss. Elle s'exprime de la manière suivante:

• Soit l'équation a.x + b.y = c où a, b et c sont des entiers de Gauss. Soit d le pgcd de a et b. Alors cette équation admet des solutions dans l'anneau des entiers de Gauss si, et seulement si, c est un multiple de d.

La démonstration est élémentaire, une division par d ramène au cas ou a et b n'ont pas de diviseurs communs autres que les éléments inversibles. L'ensemble des éléments z de la forme z = a.x + b.y est un idéal contenant celui engendré par a et celui engendré par b, il est donc engendré par un diviseur de a et de b, c’est-à-dire une unité. Or l'idéal engendré par une unité est l'anneau entier et 1 est solution de l'équation.

Lemme d'Euclide

Le lemme d'Euclide indique que :

• Si un entier de Gauss a divise un produit d'entiers de Gauss b.c et si a n'a de diviseurs en communs avec b que des éléments inversibles, alors a divise c.

La démonstration est la copie exacte du cas des entiers relatifs. Cette propriété est vraie pour tous les anneaux euclidiens.

Gauss est le premier mathématicien ayant saisi la portée de ce lemme. Il garantit l'unicité de la décomposition en facteurs premiers. Ce lemme rend possible l'arithmétique tel que nous la connaissons dans Z. C'est la raison pour laquelle il prend parfois le nom de lemme de Gauss, alors qu'il était déjà connu depuis plus de deux mille ans.

Théorème fondamental de l'arithmétique

Des nombres premier de Gauss avec "petit" norme.

Le théorème fondamental de l'arithmétique s'énonce encore exactement comme dans le cas des entiers relatifs :

• Chaque entier de Gauss peut être écrit comme un produit de nombres premiers aux éléments inversibles près d'une unique façon.

Un nombre premier de Gauss est un élément qui n'admet comme diviseur que le produit de lui-même par une unité ou une unité et qui n'est pas une unité. L'expression aux éléments inversibles près signifie que la subsitution d'un facteur irréductible par un autre facteur irréductible ne différant que par le produit d'une unité n'est pas considérée comme une décomposition différente.

Une fois encore la démonstration est la copie exacte du cas des entiers relatifs, et la propriété est vraie pour tous les anneaux euclidiens. Cette propriété dépasse le cas des anneaux euclidiens, par exemple l'anneau des polynômes sur Z vérifie cette propriété mais n'est pas euclidien. Un tel anneau s'appelle un anneau factoriel.

Un anneau satisfaisant ce théorème dispose alors des notions de ppcm et pgcd et le passage au quotient donne accès à une arithmétique modulaire de même nature que celle des entiers relatifs.

La connaissance fine de cette arithmétique suppose une capacité à caractériser les nombres premiers de Gauss.