Équation d'état de Murnaghan - Définition
La liste des auteurs de cet article est disponible ici.
Expressions de l'équation d'état
De manière générale, à température constante, le module d'incompressibilité est défini par
-
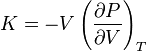
La manière la plus simple d'obtenir une équation d'état liant P et V consiste à supposer que K est constant, c'est-à-dire indépendant de la pression et de la déformation du solide. Dans cette hypothèse, le volume décroit exponentiellement avec la pression. Ce n'est pas un résultat satisfaisant car il est expérimentalement établi que plus on comprime un solide, plus il devient difficile de le comprimer. Pour aller plus loin il faut donc prendre en compte les variations des propriétés élastiques du solide avec la compression.
L'hypothèse de Murnaghan est de supposer que le module d'incompressibilité est une fonction linéaire de la pression :
L'équation de Murnaghan est le résultat de l'intégration de cette équation différentielle :
On peut également exprimer le volume en fonction de la pression :
Cette présentation est dénoncée par Poirier comme manquant de rigueur.
La même relation peut être démontrée de manière différente en partant du fait que le produit du module d'incompressibilité par le coefficient de dilatation thermique ne dépend pas de la pression pour un matériau donné.
Dans certaines circonstances, en particulier en lien avec les calculs ab initio, on préfèrera l'expression de l'énergie en fonction du volume, qui peut s'obtenir en intégrant l'équation précédente selon la relation P = − dE / dV :
Extensions et généralisations
Afin d'améliorer les modèles ou échapper aux critiques signalées plus haut, plusieurs généralisations de l'équation de Murnaghan ont été proposées. Elles consistent habituellement en l'abandon d'une hypothèse simplificatrice et l'ajout d'un paramètre indépendant supplémentaire. Ceci peut améliorer les qualités des affinements, mais complique les expressions.
Une première sophistication consiste à ajouter un terme en P2 au développement précédent en posant K = K0 + PK0' + P2K0''. La résolution de cette équation différentielle donne l'équation de Murnaghan au second-ordre :
pour Γ2 = K0'2 − 2K0K0'' > 0. On retrouve naturellement l'équation au premier ordre en prenant K0'' = 0. Des développements à un ordre supérieur à 2 sont possibles en principe, mais au prix de l'ajout d'un paramètre ajustable pour chaque terme, ce qui n'est pas forcément pertinent.
D'autres généralisations peuvent également être citées :
- Kumari et Dass ont proposé une généralisation en abandonnant la condition K'' = 0 mais en supposant le rapport K'' / K' indépendant de la pression.
- Kumar a proposé une généralisation en prenant en compte une dépendance du paramètre d'Anderson en fonction du volume. Il a été montré par la suite que cette équation généralisée n'était pas nouvelle mais se ramenait à l'équation de Tait.
Avantages et limites
En dépit de sa simplicité, l'équation de Murnaghan est en mesure de reproduire les données expérimentales dans une gamme de pression qui peut être assez large, de l'ordre de K0 / 2 selon Anderson. On peut également retenir qu'elle reste satisfaisante tant que la compression V / V0 reste supérieure à 90% environ. Dans cette gamme, l'équation de Murnaghan présente un avantage par rapport aux autres équations d'état si l'on souhaite pouvoir exprimer le volume en fonction de la pression. Néanmoins, plusieurs exemples ont montré que d'autres équations permettaient d'obtenir des affinements de meilleure qualité.
Malgré cela, plusieurs arguments théoriques et expérimentaux montrent que l'équation de Murnaghan reste insatisfaisante. Ainsi, dans la limite des très fortes compressions, on s'attend à ce que le solide se comporte comme un gaz d'électrons pour lequel K' est égal à 5/3 ; c'est la limite de Thomas-Fermi. Or, dans l'équation de Murnaghan, K' est constant et fixé à sa valeur initiale. Sauf à poser systématiquement K'0 = 5 / 3, on a donc l'assurance que l'équation de Murnaghan est inopérante dans le régime des très fortes compressions. De fait, lorsqu'il est extrapolé, le comportement prédit par l'équation de Murnaghan devient assez rapidement invraisemblable.
Indépendamment de cet argument théorique, l'expérience montre clairement que K' décroit avec la pression, ou en d'autres termes que la dérivée seconde du module d'incompressibilité K'' est non nulle et négative. Un développement à l'ordre 2 basé sur le même principe (cf. section suivante) permet de tenir compte de cette observation, mais cette solution reste encore insatisfaisante. En effet, elle conduit à un module d'incompressibilité qui devient négatif dans la limite où la pression tend vers l'infini. De fait, c'est une contradiction inévitable quel que soit le développement polynomial choisi, car on aura toujours un terme dominant, divergeant à l'infini.
Enfin, une limitation tout à fait générale de ce type d'équation d'état est leur incapacité à prendre en compte les transitions de phases induites par la pression et la température : la fusion, mais aussi les multiples transitions solide-solide qui peuvent provoquer des changements abrupts de la densité et du module d'incompressibilité en fonction de la pression.
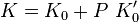
![P(V) = \frac{K_0}{K_0'} \left[\left(\frac{V}{V_0}\right)^{-K_0'} - 1\right]](https://static.techno-science.net/illustration/Definitions/autres/5/596890cb79374e281b379a2c904ae721_7ff683b9bd7a5f9e50056a348753498c.png)
![V(P) = V_0 \left[1+ P \left(\frac{K'_0}{K_0}\right)\right]^{-1/K'_0}](https://static.techno-science.net/illustration/Definitions/autres/3/38fcafdbca7175774993e03affbb4b39_c518d649c7de00691612bb723e15cb2c.png)
![E(V) = E_0 + K_0\,V_0\left[\frac{1}{K_0'(K_0'-1)}\left(\frac{V}{V_0}\right)^{1-K_0'} + \frac{1}{K_0'}\frac{V}{V_0} - \frac{1}{K_0'-1}\right].](https://static.techno-science.net/illustration/Definitions/autres/a/a61ad8405f40bf4bdd1ffe94091aac6f_1db3ef115832aebcbde7372d0c768d37.png)
![P(V) = 2 \frac{K_0}{K_0'} \left[\frac{\Gamma}{K_0'}\,\frac{(\frac{V_0}{V})^{\Gamma}+1}{(\frac{V_0}{V})^{\Gamma}-1} - 1\right]^{-1}](https://static.techno-science.net/illustration/Definitions/autres/b/bb17d54e8866a8c1b7a31494b33dae89_9bad26dec06f7d5492884e9e389fa0b6.png)