Espace vectoriel normé - Définition

Topologie

Topologie d'un sous-espace, produit, quotient

Comme le montre l'article norme, la norme sur un espace vectoriel induit une topologie, pour laquelle l'addition et la multiplication externe sont continues.

Un sous-espace vectoriel F hérite donc de deux topologies : la topologie issue de sa norme (restriction de la norme sur l'espace entier) et la topologie induite par celle de l'espace vectoriel. Ces deux topologies sur F sont en fait égales ; en effet, elles possèdent toutes les deux comme base de voisinages d'un point x de F l'intersection des boules ouvertes de centre x avec F. Or deux topologies ayant, pour chaque point, une même base de voisinages, sont confondues.

La configuration est la même pour le produit de deux espaces E et F. Pour la norme définie précédemment, les boules de centre (x,y) et de rayons r>0 (qui constituent une base de voisinages de (x,y) pour la topologie associée à cette norme) ne sont autres que les , donc constituent également une base de voisinages pour la topologie produit. Remarquons l'adéquation de la définition de à partir de et , qui pouvait a priori sembler arbitraire. Mais signalons que la même topologie sur est obtenue en posant où N est une norme quelconque sur , par exemple l'une des normes usuelles mentionnées plus haut. Ceci est dû au fait que N est toujours équivalente à la norme max utilisée ici.

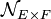
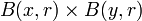
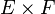
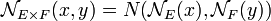
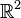
La situation reste analogue pour un quotient E/F. En effet, si φ est la projection canonique de E dans E/F, une base de voisinages de φ(x) pour la topologie quotient est constituée des φ(B(x,r)) (pour r>0), qui coïncident exactement avec les boules (dans E/F, pour la semi-norme induite) de centre φ(x) et de rayon r.

Ainsi, la topologie induite sur un sous-espace, un produit d'espaces ou un quotient coincide avec celle issue de la norme induite (ou de la semi-norme induite, dans le cas d'un quotient par un sous-espace non fermé).

Opérateur borné

Un opérateur borné entre deux espaces vectoriels normés est simplement une application linéaire continue. Cette double appellation est justifiée par la proposition suivante (dont la démonstration, classique pour K=R, se généralise) :

La norme d'opérateur d'un tel f est la plus petite constante C telle que f soit C-lipschitzienne. Dans l'espace vectoriel L(E, F) des applications linéaires de E dans F, le sous-espace vectoriel de celles qui sont continues se note (ou parfois L_c(E,F)). La norme d'opérateur en fait un espace vectoriel normé.

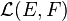
Complétude

Un espace vectoriel normé complet porte le nom d'espace de Banach. Un espace vectoriel normé n'est pas nécessairement complet, c'est-à-dire que les suites de Cauchy ne sont pas nécessairement convergentes. Par exemple, l'espace préhilbertien engendré par les polynômes trigonométriques n'est pas complet. De manière plus générale :

Le complété d'un espace vectoriel normé jouit de propriétés supplémentaires par rapport au complété d'un simple espace métrique :

En général, E est identifié à son image J(E) dans E_c. Ainsi, E apparait comme un sous-espace vectoriel de E_c, et la norme sur E induite par la norme de E_c coïncide avec la norme originelle sur E car J est une isométrie.

Le remplacement d'un espace E par son complété E_c ne modifie pas l'espace des applications linéaires de E dans F si F est complet (cette propriété permet de montrer que la proposition précédente caractérise l'espace vectoriel normé E_c à isomorphisme près) :

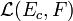
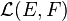
La complétude de F se transmet à l'espace des applications linéaires continues à valeurs dans F.

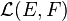
• Un espace vectoriel normé réel de base dénombrable n'est pas complet :

Soit E un espace de base . Pour tout entier n, notons E_n le sous-espace vectoriel engendré par . Alors E est la réunion des E_n, qui sont fermés (car de dimension finie, cf dernier paragraphe) et dont les intérieurs sont vides. Or E est, lui, d'intérieur non vide. D'après le théorème de Baire, E est donc non complet.

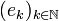
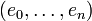
• Il existe un espace vectoriel normé complet E_c et une isométrie linéaire J, de E dans E_c, dont l'image est dense dans E_c :

Le complété de E est, comme le complété de tout espace métrique, un espace métrique complet F muni d'une application isométrique J de E dans F, d'image dense. De plus ici, F est (par construction) le quotient de l'espace vectoriel des suites de Cauchy à valeurs dans E, muni de la semi-norme q définie par , par le sous-espace vectoriel des suites x telles que q(x) = 0. F est donc naturellement muni d'une structure d'espace vectoriel normé, et la métrique de F n'est autre (par construction encore) que celle induite par sa norme.

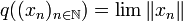
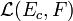
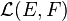
• Soient E de complété E_c, et F complet. Alors l'application "restriction", de dans , est un isomorphisme isométrique :

Les deux seuls points délicats sont la surjectivité de cette application -- notons-la R -- et le fait que . Il s'agit donc de prouver que toute application linéaire continue g de E dans F se prolonge en une application linéaire f de E_c dans F, de norme majorée par celle de g. D'après la propriété qui caractérise le complété d'un espace métrique, on sait déjà (puisque g est uniformément continue) que g admet un prolongement f continu. La linéarité de f se déduit alors de celle de g par densité de E. La majoration de sa norme s'obtient également par densité.

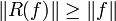
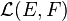
• Soient E et F deux espaces vectoriels normés. Si F est complet alors l'espace muni de la norme des opérateurs est complet.

En effet, s'identifie à un sous-espace fermé d'un espace complet : en notant B la boule unité de E, l'application restriction, de dans l'espace (complet) des applications continues bornées de B dans F, est une isométrie d'image fermée.

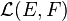
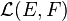
Plus élémentairement, soit (u_n) une suite de Cauchy d'applications linéaires continues de E dans F et x un vecteur de E. La suite (u_n(x)) vérifie la propriété suivante :

Elle est donc de Cauchy, comme E est complet elle converge. Notons u(x) cette limite. Elle définit une fonction u de E dans F, qui est limite simple des u_n, donc linéaire elle aussi ; de plus, comme (u_n) est une suite de Cauchy, elle est bornée par un certain λ, d'où et donc par passage à la limite sur n, on obtient , ce qui montre la continuité de u. On montre enfin que (u_n) converge vers u dans  : pour ε > 0, il existe n₀ dans tel que en passant à la limite sur m, on déduit d'où Ceci achève la seconde démonstration.

 

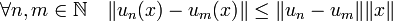
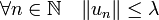
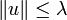
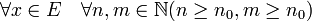
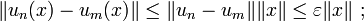
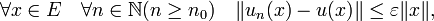
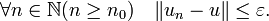
Théorème de Riesz

Ce théorème stipule que si la boule unité (fermée) d'un espace vectoriel normé E réel ou complexe est compacte, alors E est de dimension finie.

Autrement dit, la boule unité fermée d'un espace vectoriel normé de dimension infinie est toujours non compacte.
Cependant, la boule unité fermée de son dual topologique (de dimension infinie également) est faiblement compacte, c'est-à-dire compacte pour la topologie faible.