Fonction de Möbius - Définition

Combinatoire

Définitions et propriétés élémentaires

Une première approche, pour démontrer les formules du paragraphe précédent consiste à utiliser un raisonnement combinatoire. La technique consiste à étudier un ensemble A fini et ordonné par une relation d'ordre notée ≤. On utilise la définition suivante :

Définition d'une chaîne — Soient p un nombre entier et (a, b) un couple d'éléments de A tel que a ≤ b. On appelle chaîne de longueur p, joignant a à b, toute suite finie (x₀, x₁, ..., x_p) telle que :

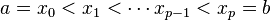
Dans la suite du paragraphe, on note c_p(a, b) le nombre de chaînes de longueur p reliant a à b. On dispose immédiatement de quelques propriétés. Par exemple, si a est un élément de A, c₀(a, a) = 1, c_p(a, a) = 0 si p est différent de 0, si b est un élément de A strictement plus grand que a alors c₀(a, b) = 0 et c₁(a, b) = 1. Un peu de réflexion permet d'établir par récurrence la proposition suivante :

Proposition 1 — Si a et b sont deux éléments de A tels que b est strictement plus grand que a et p un nombre entier positif :

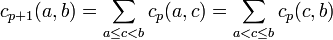
Par analogie avec la définition précédente, le mathématicien G. C. Rota définit une nouvelle fonction de Möbius, qu'il note μ_A :

Définition de G. C. Rota de la fonction de Möbius μ_A — La fonction de Möbius μ_A est définie de AxA à valeurs dans les entiers par l'égalité :

Autrement dit, on compte positivement toutes les chaînes de longueurs paires reliant a à b et négativement celles de longueurs impaires. On remarque de plus que ces définitions restent valables si A est infini, à condition qu'il n'existe qu'un nombre fini d'éléments situés entre a et b. La proposition 1 permet de démontrer la :

Proposition 2 — Soient a et b deux éléments de A tel que a soit strictement plus petit que b :

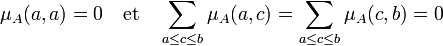
• Si a et b sont deux éléments de A tels que b est strictement plus grand que a et p un nombre entier :

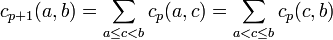
Toute chaine de longueur p + 1 joignant a à b est composée d'une chaîne de longueur p reliant a à c et d'une chaîne de longueur 1 reliant c à b, ce qui démontre la première égalité. La deuxième se montre de la même manière.

• Soient a et b deux éléments de A tel que a soit strictement plus petit que b :

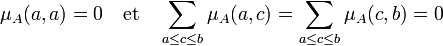
La première égalité provient d'une fait que l'unique chaîne reliant a à a est de longueur 0. La deuxième est une conséquence directe de la proposition précédente :

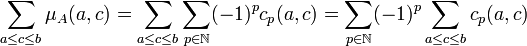
La proposition précédente montre que :

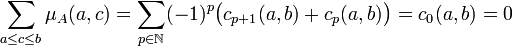
La dernière égalité se montre de la même manière.

 

Formule d'inversion de Rota

L'un des intérêts de la fonction de Möbius est la formule d'inversion associée. Les résultats du paragraphe précédent permettent de l'établir. Soient G un groupe additif, c'est-à-dire un groupe abélien dont l'opération est notée additivement et f une fonction de A dans G. On peut considérer par exemple de G est égal à Z, le groupe des nombres entiers. Soit g la fonction définie par :

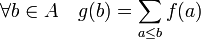
On se trouve alors dans une configuration analogue à celle de la formule d'inversion de Möbius.

Formule d'inversion de Rota — L'égalité suivante est vérifiée :

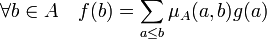
Cette formule reste vraie si A n'est pas de cardinal fini, mais s'il n'existe qu'un nombre fini d'éléments de A plus petits qu'un élément b donné.

• L'égalité suivante est vérifiée :

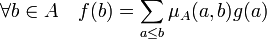
Il suffit pour s'en rendre compte de regrouper différemment les termes de la somme de droite :

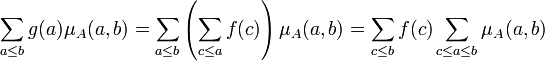
Les termes de droites sont tous nuls, sauf si c est égal à b, a est alors aussi égal à b et μ_A(a, a) est égal à 1, ce qui montre le résultat.

 

Relation entre la définition de Möbius et celle de Rota

Ici, l'ensemble A désigne celui des entiers strictement positifs munis de la relation d'ordre : a ≤ b lorsque a est un diviseur de b. On dispose de la propriété :

Relation entre les définitions des fonctions de Möbius — Soit a et b deux entiers tels que a divise b. Si la fonction μ désigne celle de Möbius, on dispose des égalités :

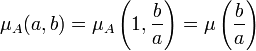
La définition de la fonction de Möbius donnée initialement apparaît comme un cas particulier de celle de Rota. En conséquence, la démonstration de la relation du paragraphe implique celle de la formule d'inversion de Möbius.

• L'égalité suivante est vérifiée :

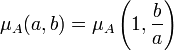
Il suffit pour cela de montrer qu'il existe une bijection entre l'ensemble des chaines de longueurs p reliant a à b et celles reliant 1 à b/a. Cette bijection est très naturelle, à une chaîne (x₁, x₁,..., x_p) reliant a et b, on associe la chaîne (1, x₂/x₁,..., x_p/x₁). Cette application est manifestement une bijection, ce qui montre la proposition.

• L'égalité suivante est vérifiée :

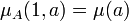
Soit s le nombre de nombres premiers qui divisent a, compté avec leur multiplicité. C'est-à-dire que si p₁, ...p_s sont ces nombres premiers, on dispose de l'égalité :

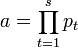
On raisonne par récurrence sur s. Si s est égal à 0, alors a est égal à 1 et l'égalité est vérifiée. Supposons la propriété vraie pour s et montrons là pour s + 1. Avec les notations précédentes, le théorème 1 montre que :

L'hypothèse de récurrence montre que :

La proposition 2 montre que :

On en déduit l'égalité recherchée.