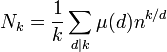Fonction de Möbius - Définition

Usages

Arithmétique modulaire

La convolution de Dirichlet permet de démontrer aisément quelques formules d'arithmétiques. Soit φ la fonction qui à un entier strictement positif n associe le nombre d'entiers inférieurs à n et premiers avec n. Cette fonction est aussi celle qui à n associe le nombre d'élément générateurs du groupe cyclique d'ordre n. Elle est appelée indicatrice d'Euler.

Tout élément d'un groupe cyclique est générateur d'un sous-groupe cyclique. Dans un groupe cyclique d'ordre n, il existe exactement autant de sous-groupes que de diviseurs de n et l'ordre de chacun des sous-groupes peut être choisi égal à ce diviseur. Si les éléments du groupe sont partitionnés par la relation d'équivalence : g est en relation avec h lorsque g et h engendrent le même sous-groupe, on obtient l'égalité sur l'ordre n du groupe cyclique :

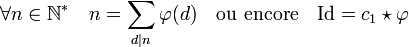
Ici, Id désigne la fonction arithmétique identité, qui à n associe n. La fonction de Möbius permet de déterminer une expression de l'image d'un entier strictement positif n par l'indicatrice d'Euler. Une convolution par μ, appliquée à l'égalité Id = c₁ * φ donne : φ = μ * Id, égalité qui s'écrit :

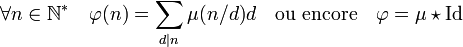
A ce stade, rien n'indique encore que φ est une fonction multiplicative. Cependant, la loi * s'applique à toute fonction arithmétique, c'est-à-dire à toute fonction de N^* dans un groupe abélien, ici Z. Sur cet ensemble, la loi * est associative, ce qui autorise le calcul précédent. Soit p un nombre premier et s un entier strictement positif; La formule précédente montre que :

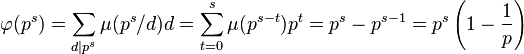
La fonction φ est égal à la convolution de Id et de la fonction de Möbius, deux fonctions multiplicatives, c'est donc une fonction multiplicative. Cette remarque permet de terminer le calcul. Soit n un entier strictement plus grand que 1, p_i, pour i variant de 1 à m les nombres premiers qui divisent n et s_i l'exposant de p_i dans la décomposition en facteurs premiers de n.

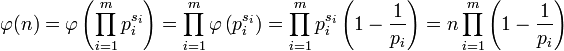
Polynôme cyclotomique

La formule d'inversion de Möbius est valable pour toute fonction f de N^* dans un groupe abélien. Si la notation est multiplicative, la formule devient :

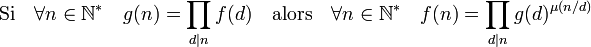
Soit K un corps premier, celui des rationnels ou F_p le corps contenant p éléments. Ici n désigne un entier strictement positif et Φ_n(X) le polynôme cyclotomique d'indice n à coefficient dans K. Si K est égal à F_p, n est choisi premier avec p. On dispose de l'égalité :

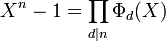
Si la fonction f est à valeurs dans le groupe multiplicatif des fractions rationnelles non nulles à coefficients dans K et si elle associe à d le polynôme cyclotomique Φ_d(X), l'égalité précédente montre que la fonction g est celle qui associe à d la fraction X^d - 1. La formule d'inversion de Möbius donne un moyen de calculer le polynôme cyclotomique d'indice n.

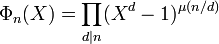
Polynôme irréductible et corps fini

La fonction de Möbius joue un rôle dans des problèmes de dénombrements. Certains codes correcteurs, comme les codes cycliques sont construits à l'aide de l'anneau des polynômes formels à coefficients dans un corps fini F_n et d'un polynôme irréductible et unitaire de degré k, où k est premier avec n. Pour cette raison, il est utile de connaître le nombre N_k de polynômes irréductibles unitaires de degré k à coefficients dans F_n. Ici, F_n désigne le corps à n éléments. Cette question est un exemple de problème de dénombrement fait intervenir la fonction de Möbius.

Soit P(X) l'un des polynômes recherchés. Ce polynôme n'admet que des racines distinctes, toutes sont éléments du corps à n^k éléments. Le groupe multiplicatif d'un corps fini est cyclique, autrement dit, le polynôme X^nk-1 - 1 admet pour racines tous les éléments non nuls du corps à n^k éléments. Le polynôme X^nk - X admet pour racines exactement tous les éléments du corps. Ce qui revient à dire que ce polynôme est divisible par tous les polynômes irréductibles de degré k. On considère sa décomposition en polynômes irréductibles unitaires à coefficients dans F_n :

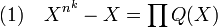
Montrons que le degré d d'un facteur Q(X) de droite divise k. Soit K le corps de rupture de Q(X), son cardinal est égal à n^d. Le corps à n^k éléments peut être considéré comme un espace vectoriel sur K, son cardinal est donc de la forme n^d.a, où a est un entier strictement positif. Comme ce cardinal est aussi égal à n^k, on en déduit que d.a = k.

L'égalité (1) est formée, à droite d'exactement N_d facteurs irréductibles unitaires de degré d. L'égalité sur les degrés se traduit par :

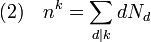
Soit f la fonction arithmétique qui à d associe d.N_d et g celle qui à d associe n^d. La formule d'inversion de Möbius s'écrit :

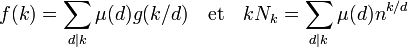
On en déduit la formule suivante: