Fonction de Möbius - Définition
La liste des auteurs de cet article est disponible ici.
Convolution de Dirichlet
Contexte
Il existe une manière moins combinatoire et plus arithmétique d'étudier la fonction de Möbius. Le contexte est un peu plus abstrait, la structure de base est celle des fonctions multiplicatives munies d'une opération binaire : la convolution de Dirichlet. Soit M l'ensemble des fonctions multiplicatives, c'est-à-dire des fonctions définies sur N* à valeurs dans les nombres complexes qui valent 1 en 1 et telles que si a et b sont deux entiers strictement positifs premiers entre eux, f(a.b) = f(a).f(b).
La convolution de Dirichlet, notée dans cet article *, associe à deux éléments de M, f et g la fonction f * g définie par :
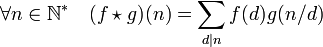
La convolution de Dirichlet possède suffisamment de bonnes propriétés pour rendre le concept fructueux. Tout d'abord, elle définit une loi interne sur M, c'est-à-dire que la convolution de deux fonctions multiplicatives est encore une fonction multiplicative. Ensuite, la loi est commutative et associative. Enfin, il existe un élément neutre, notée ici 1M, c'est la fonction qui à 1 associe 1 et à tout autre élément associe 0, et tout élément de M possède un symétrique. Autrement dit, la structure (M, *) est celle d'un groupe abélien.
Étudier la fonction de Möbius sous cet angle apporte un éclairage différent sur les propriétés de la fonction. D'un côté, on perd en généralité par rapport à l'approche de Rota. L'approche par la convolution de Dirichlet ne s'applique qu'aux entiers strictement positifs munis de l'ordre induit par la division, restriction que n'a pas celle de Rota. Ensuite, le cadre conceptuel est plus abstrait, on utilise ici une structure abstraite, celle d'un groupe abélien particulier. En revanche, les définitions sont plus naturelles avec la convolution de Dirichlet. Des propriétés qui apparaissent comme un peu magiques avec l'approche combinatoire deviennent plus intuitives. Enfin, certains résultats plus algébriques ou arithmétiques se démontrent plus aisément avec les propriétés de la convolution.
Définition alternative
Sous l'angle du paragraphe, il existe une définition plus naturelle de la fonction de Möbius. Pour l'exprimer, une notation est utile. La fonction c1 désigne la fonction constante 1, c'est-à-dire la fonction qui à tout élément de N*, associe 1.
Définition alternative de la fonction de Möbius — La fonction de Möbius est l'inverse de la fonction c1 dans le groupe (MK, *).
Le théorème 1 devient maintenant l'élément clé de la définition. La fonction de Möbius est définie comme l'unique fonction multiplicative qui vérifie l'égalité c1 * μ = 1M, ou encore :

La définition précédente devient maintenant une proposition :
Proposition 3 — Les deux définitions de la fonction de Möbius coïncident.
Sous cet angle, la définition de la fonction de Möbius est plus naturelle, c'est l'inverse de la fonction constante 1. La formule d'inversion se démontre immédiatement. Soit f une fonction multiplicative quelconque. La fonction g associée est définie par g = c1 * f. En appliquant aux deux membres une convolution par μ, l'égalité devient f = μ * g, cette égalité est la formule d'inversion de Möbius. Avec la convolution de Dirichlet, les démonstrations sont singulièrement plus courtes.
Il suffit de montrer que les images d'une puissance d'un nombre premier par les deux fonctions sont les mêmes. En effet, tout entier strictement positif s'écrit de manière unique comme produit de puissances de nombres premiers. Ces puissances sont en effet premières entre elles deux à deux. Soit s un entier strictement positif et p un nombre premier. La fonction μ désigne ici l'inverse de 1M. Montrons par récurrence sur s que les deux valeurs coïncident. Pour s égal à 1 :
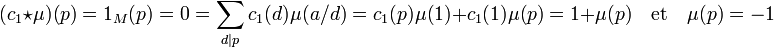
Supposons maintenant la proposition vraie pour s et montrons là pour s + 1.