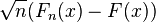Fonction de répartition empirique - Définition

Introduction

En Statistiques, une fonction de répartition empirique est une fonction de répartition qui attribue la probabilité 1/n à chacun des n nombres dans un échantillon.

Soit un échantillon de variables iid à valeurs dans avec pour fonction de répartition F(x).

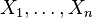
La fonction de distribution empirique F_n(x) basée sur l'échantillon est une fonction en escalier définie par

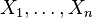
où I(A) est la fonction indicatrice de l'événement A.

Pour un x fixé, la variable est une variable aléatoire de Bernoulli, de paramètre p = F(x). Par conséquent, la variable nF_n(x) est distribuée selon une loi binomiale, avec pour moyenne nF(x) et pour variance nF(x)(1 − F(x)).

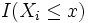
Propriétés asymptotiques

• Par la loi forte des grands nombres,

presque sûrement pour un x fixé.

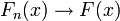
En d'autres termes, F_n(x) est un estimateur non-biaisé de la fonction de répartition F(x).

• Par le théorème de la limite centrale,

converge en loi vers une loi normale N(0, F(x)(1 - F(x))) pour un x fixé.

Le théorème de Berry–Esseen (en) procure le taux de convergence.

• Par le théorème de Glivenko-Cantelli (en) uniformément, c'est-à-dire

with probability 1.

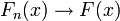
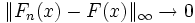
L'inégalité de Dvoretzky-Kiefer-Wolfowitz (en) procure le taux de convergence.

• Kolmogorov a montré que

converge en distribution vers la distribution de Kolmogorov, à condition que F(x) est continu.

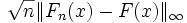
Le test de Kolmogorov-Smirnov de goodness-of-fit est basé sur ce fait.

• Par le théorème de Donsker,

, en tant que processus indexé par x, converge faiblement dans vers un pont brownien B(F(x)).

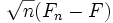
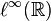
Bibliographie

• (en) Galen R. Shorack et Jon A. Wellner, Empirical Processes With Applications to Statistics, Society for Industrial & Applied Mathematics, 4 septembre 2009, 998 p.  
• van der Vaart, A.W. and Wellner, J.A. (1996) "Weak Convergence and Empirical Processes", Springer. ISBN 0-387-94640-3.